Superharmonic Instability

Originally found by:
Longuet-Higgins (1978)
Longuet-Higgins & Cokelet (1978)
⤷ using the numerical method of Longuet-Higgins & Cokelet (1976)

Later confirmed and extended by:
Tanaka (1983, 1985)
Tanaka, Dold, Lewy & Peregrine (1987)

Effects of viscosity and surface tension:
Mansar, Turner, Bridges & Dias (2025)

The geometric viewpoint

To compute the shape of the wave
Explicit interface representation
Lagrangian advection
Fails as the splash singularity occurs

The phenomenological viewpoint

To compute the energy dissipation
Implicit interface representation
Eulerian advection
Mostly two-fluids studies

On the vanishing viscosity limit up to the splash

\[\mathrm{Re} \to +\infty \]

A numerical method for the free-surface Navier-Stokes equations

Finite Element method
Arbitrary Lagrangian-Eulerian advection

Boundary layers in Water Waves

The free-surface boundary layer
Vorticity separation from the bed

Euler (+ irrotationality)

Mapping to the unit circle in \(\mathbb{C}\):
⤷Longuet-Higgins & Cokelet (1976)
The vortex and dipole methods:
⤷Baker, Meiron & Orszag (1982)
⤷Baker & Xie (2011)
⤷Dormy & Lacave (2024)
Boundary Element Methods (BEM) in 3D:
⤷Grilli, Guyenne & Dias (2001)

Navier-Stokes

Two-dimensional studies:
⤷Chen, Kharif, Zaleski & Li (1999)
⤷Deike, Popinet & Melville (2015)
Three-dimensional studies:
⤷Lubin & Glockner (2015)
⤷Deike, Melville & Popinet (2016)
⤷Mostert, Popinet & Deike (2022) ⤷Scapin et al. (2025)

Non-dimensional quantities: \[ \begin{align} \boldsymbol{x} & \to h_0 \boldsymbol{x} \\ \boldsymbol{u} & \to \sqrt{gh_0} \boldsymbol{u} \\ p & \to \rho g h_0 p \\ \end{align} \] yielding the following Reynolds number, \[ \mathrm{Re} = \frac{h_0 \sqrt{gh_0}}{\nu} \]

Incompressible, non-dimensional Navier-Stokes equations in \(\Omega(t)\) \[ \begin{align} \partial_t \boldsymbol{u} + \boldsymbol{u} \cdot \boldsymbol{\nabla} \boldsymbol{u} &= - \boldsymbol{\nabla}p + \frac{1}{\mathrm{Re}}\, \Delta \boldsymbol{u} + \boldsymbol{g} \\ \boldsymbol{\nabla} \cdot \boldsymbol{u} &= 0 \end{align} \]

Stress-free boundary condition on the free surface \[ \begin{align} p \hat{\boldsymbol{n}} - \frac{1}{\mathrm{Re}} \, \Big[ \boldsymbol{\nabla} \boldsymbol{u} + \big(\boldsymbol{\nabla}\boldsymbol{u}\big)^{\top} \Big] \, \hat{\boldsymbol{n}} &= 0 && \text{on } \Gamma_i(t) \end{align} \] Navier boundary condition on the bottom topography \(\Gamma_b = \{z = 0\}\) \[ \begin{align} \hat{\boldsymbol{\tau}}\,\Big[\boldsymbol{\nabla} \boldsymbol{u} + \big(\boldsymbol{\nabla}\boldsymbol{u}\big)^{\top}\Big] \, \hat{\boldsymbol{n}} &= 0 & u_z &= 0 \end{align} \]

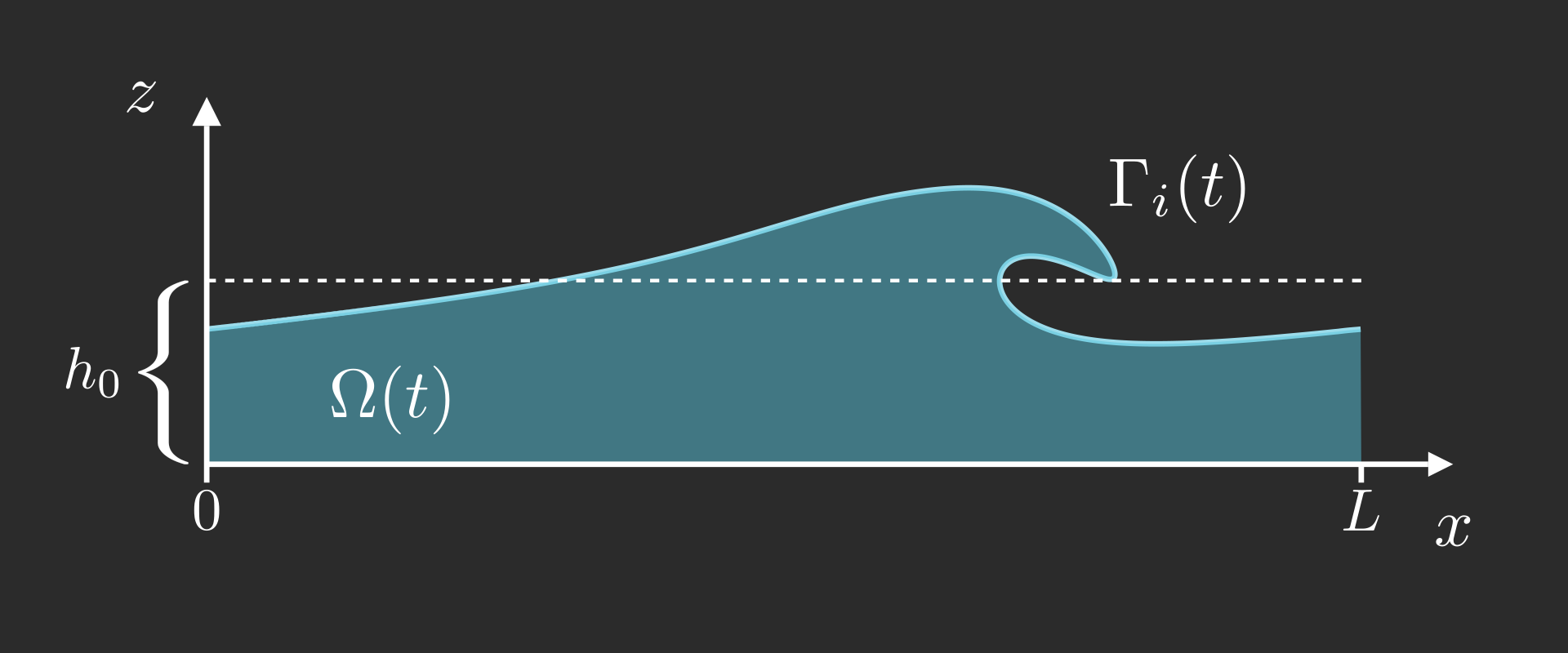
We use the first order (in \(a\)) solution (i.e. a linear wave) of amplitude \(a = 0.5\), \[ \boldsymbol{\gamma}(t=0,s) = \begin{bmatrix} s \\ h_0 + a \cos(kx) \end{bmatrix}\qquad\text{and}\qquad \boldsymbol{u}_0(x,z) = \frac{a\omega}{\sinh(kh_0)} \begin{bmatrix} \cosh(k\style{color: #42affa;}{h_0}) \cos(kx) \\ \sinh(k\style{color: #42affa;}{h_0}) \sin(kx) \end{bmatrix} \] Then we solve numerically the following elliptic problem,

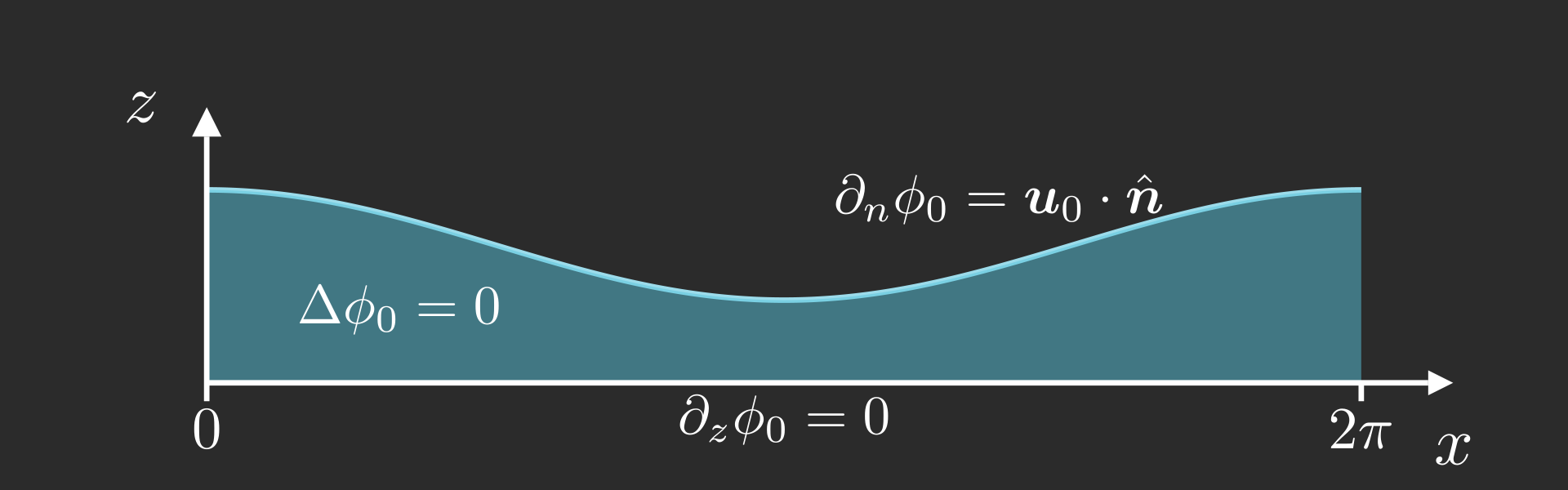
At last, the initial velocity is computed as \( \boldsymbol{u}(t = 0) = \boldsymbol{\nabla} \phi_0 \)

We represent the free surface as a parametrised curve \( \boldsymbol{\gamma}(t,s) \) whose points are advected in a Lagrangian manner, \[ \partial_t \boldsymbol{\gamma}(t,s) = \boldsymbol{u}\big( t, \boldsymbol{x} = \boldsymbol{\gamma}(t,s) \big) \]

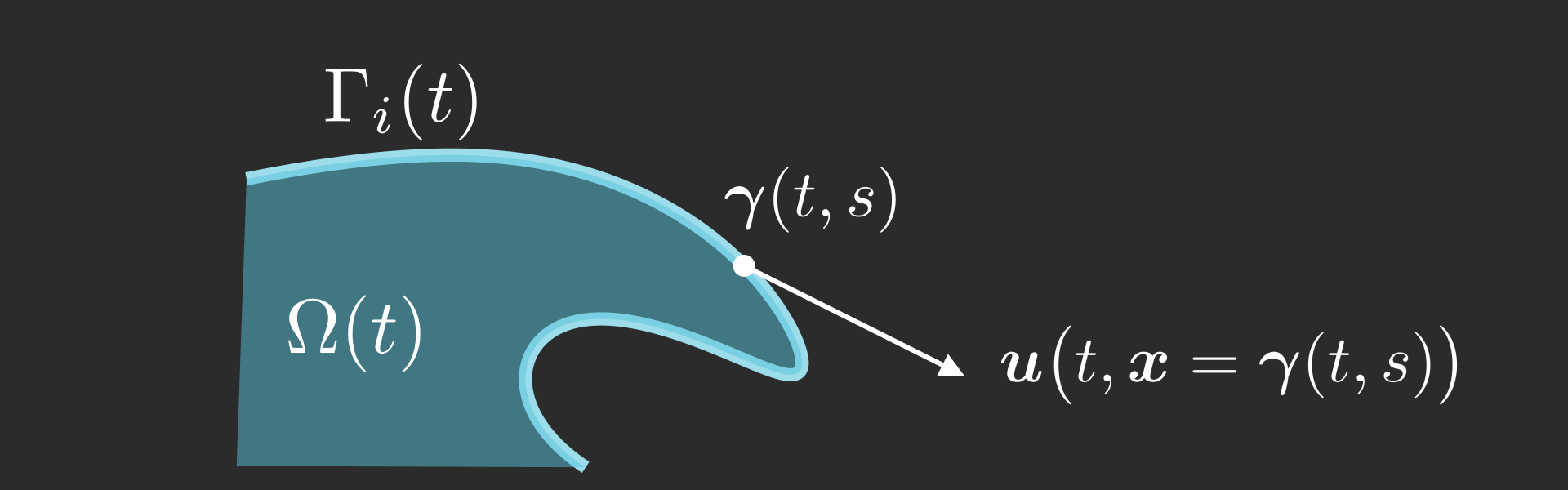
We use the FreeFEM library Hecht (2012) to

generate and handle the mesh
build and handle the matrices
use the PETSc methods easily

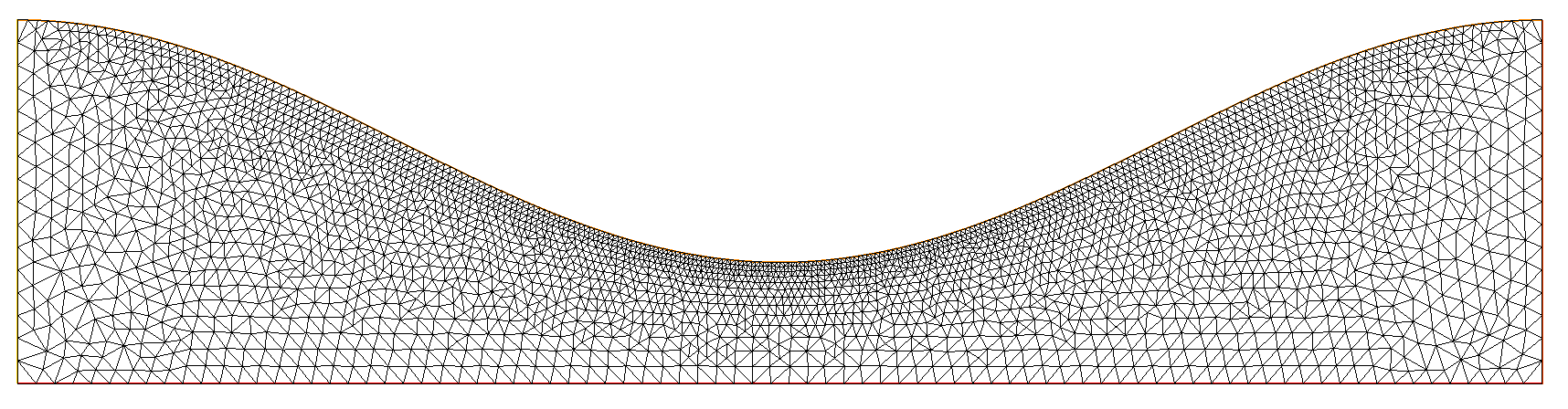
Figure - The mesh generated from the initial free surface (\(\approx 200\,000\) triangles).

We look for a velocity \( \boldsymbol{u} \) in the function space \[ \mathbf{H}^1_{\Gamma_b} = \Big\{ \boldsymbol{v} \text{ is differentiable once & such that } \boldsymbol{v} \cdot \hat{\boldsymbol{n}} = 0 \text{ on } \Gamma_b \Big\} \] Note that the incompressibility is not assumed in the function space.

Find \( (\boldsymbol{u}, p) \) such that, \[ \int_{\Omega(t)} \boldsymbol{v} \cdot \partial_t \boldsymbol{u} + \boldsymbol{v} \cdot \big( \boldsymbol{u} \cdot \boldsymbol{\nabla} \boldsymbol{u} \big) + \frac{2}{\mathrm{Re}}\, \mathsf{S}(\boldsymbol{v}):\mathsf{S}(\boldsymbol{u}) - p \boldsymbol{\nabla}\cdot\boldsymbol{v} + q \boldsymbol{\nabla}\cdot\boldsymbol{u} - \boldsymbol{v} \cdot \boldsymbol{g} = 0 \] for all \( (\boldsymbol{v}, q) \) and at all time \(t\in(0,T)\).

Find \( (\boldsymbol{u}, p) \) such that, \[ \int_{\Omega(t)} \boldsymbol{v} \cdot \partial_t \boldsymbol{u} + \boldsymbol{v} \cdot \big( \boldsymbol{u} \cdot \boldsymbol{\nabla} \boldsymbol{u} \big) + \frac{2}{\mathrm{Re}}\, \mathsf{S}(\boldsymbol{v}):\mathsf{S}(\boldsymbol{u}) - p \boldsymbol{\nabla}\cdot\boldsymbol{v} + q \boldsymbol{\nabla}\cdot\boldsymbol{u} - \boldsymbol{v} \cdot \boldsymbol{g} = \frac{1}{\mathrm{Bo}} \int_{\Gamma_i(t)} \kappa \boldsymbol{v} \cdot \hat{\boldsymbol{n}} \] for all \( (\boldsymbol{v}, q) \) and at all time \(t\in(0,T)\).

The Arbitrary Lagrangian-Eulerian Method (ALE)

⤷Hirt, Amsden & Cook (1974)

In our case, we compute the mesh's velocity by numerically solving the following elliptic problem at each time step, \[ \left\{ \begin{array}{rcll} \Delta \boldsymbol{w} &=& 0 & \text{in the domain } \Omega(t) \\ \boldsymbol{w} &=& \boldsymbol{u} & \text{on the free surface } \Gamma_i(t) \\ \boldsymbol{w} &=& 0 & \text{on the bottom } \Gamma_b \\ \end{array} \right. \]

We use a backward Euler (implicit) scheme for all terms but the non-linearity, \[ \frac{\boldsymbol{u}^{n+1} - \boldsymbol{u}^{n}}{\delta t} + (\boldsymbol{u}^{n} - \boldsymbol{w}^{n}) \cdot \boldsymbol{\nabla} \boldsymbol{u}^{n+1} = - \boldsymbol{\nabla} p^{n+1} + \frac{1}{\mathrm{Re}}\, \Delta \boldsymbol{u}^{n+1} - \hat{\boldsymbol{z}} \] \[ \boldsymbol{\nabla} \cdot \boldsymbol{u}^{n+1} = 0 \]

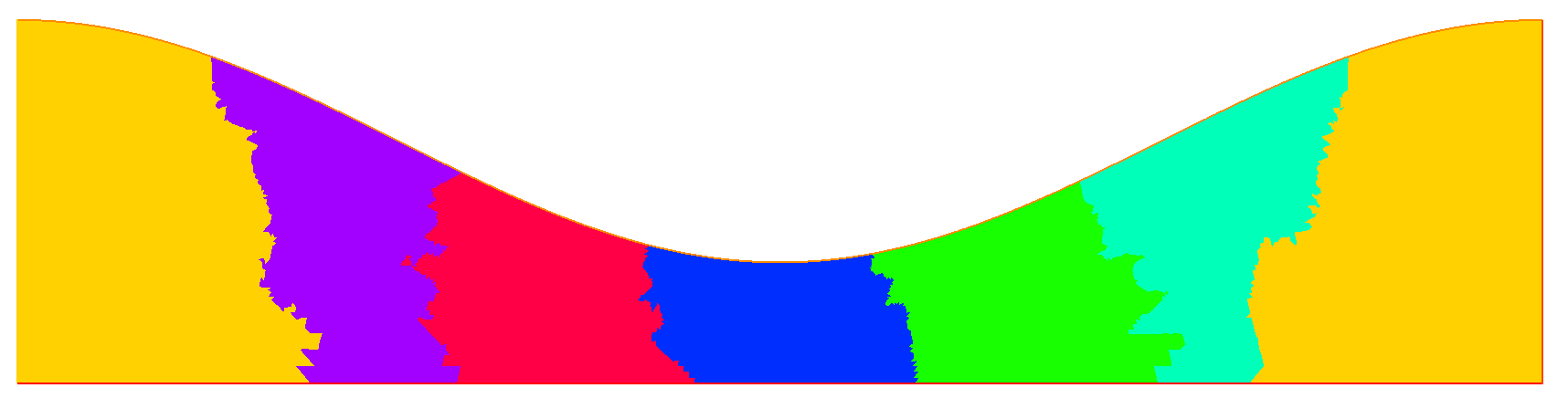
Figure - Sample domain decomposition with 6 MPI processes.

Figures - Sample domain decomposition with 6 MPI processes.

The vanishing viscosity limit in water waves up to the splash

\[\mathrm{Re} \to +\infty \]

Numerical method for the free-surface Navier-Stokes system

Finite Element method
Arbitrary Lagrangian-Eulerian advection

Breaking waves at high Reynolds number

Convergence to the inviscid system?
Surface boundary layer

Animated Figure (from R. & Dormy (2024)) - Interface evolution for a Reynolds number \(\mathrm{Re} = 10^6\)

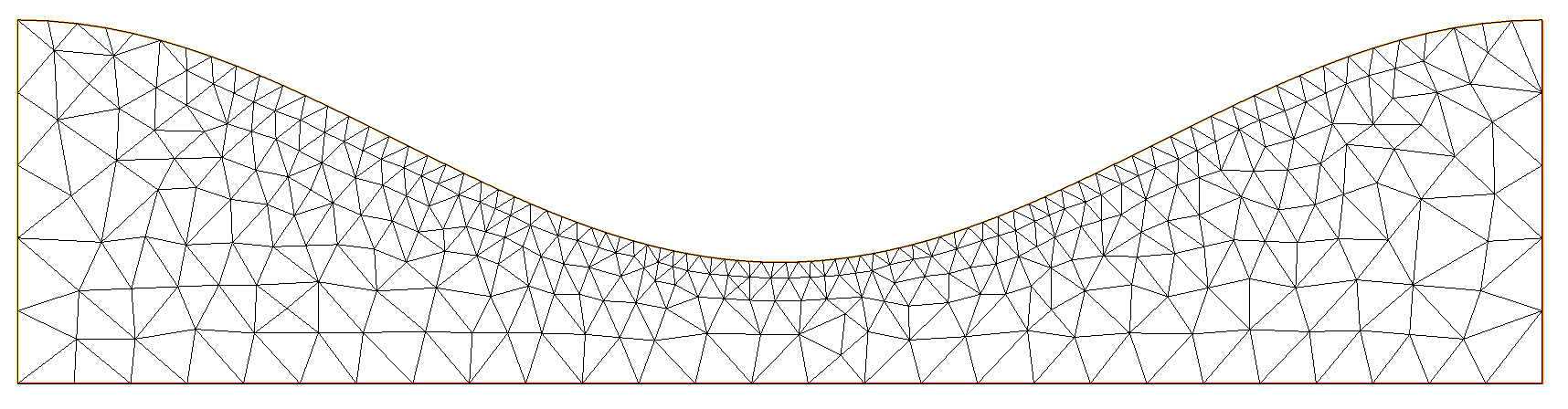
Figure - The mesh close to the end of the simulation shown before.

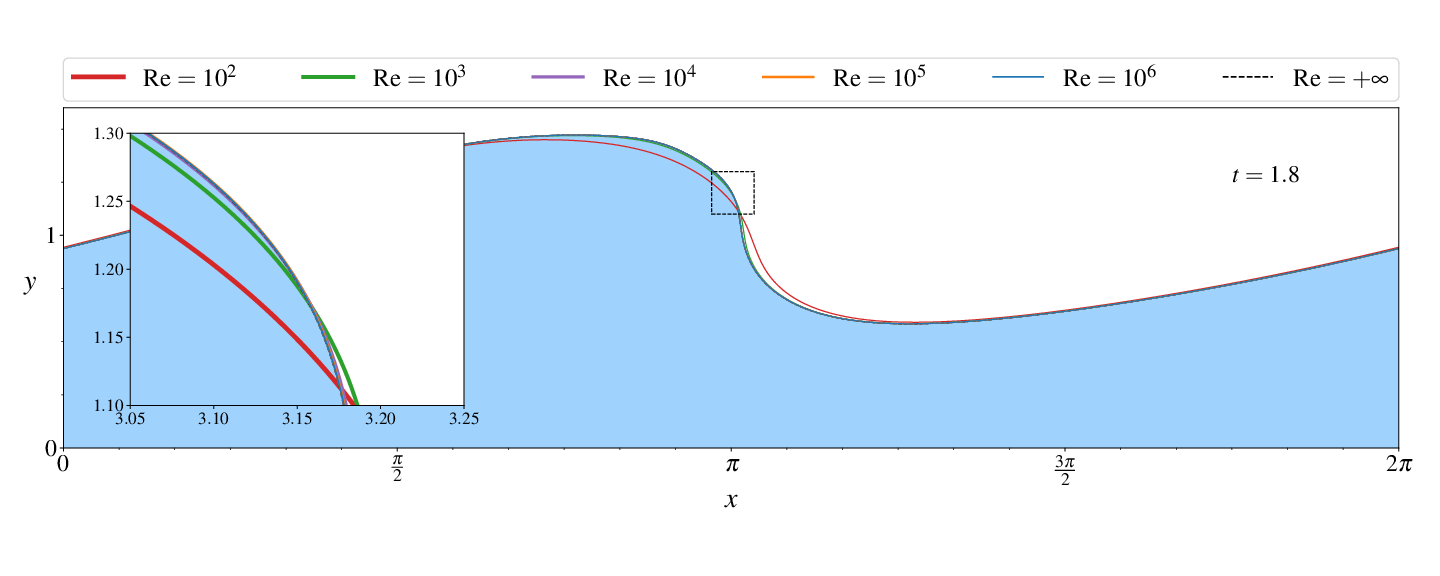
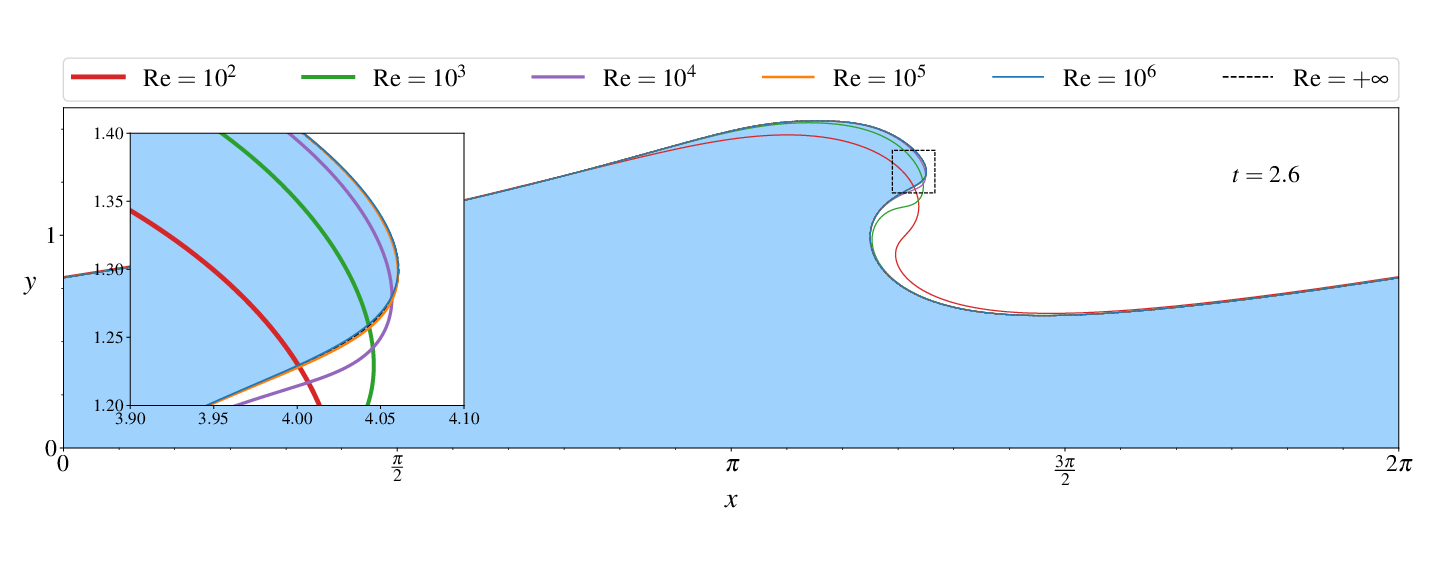
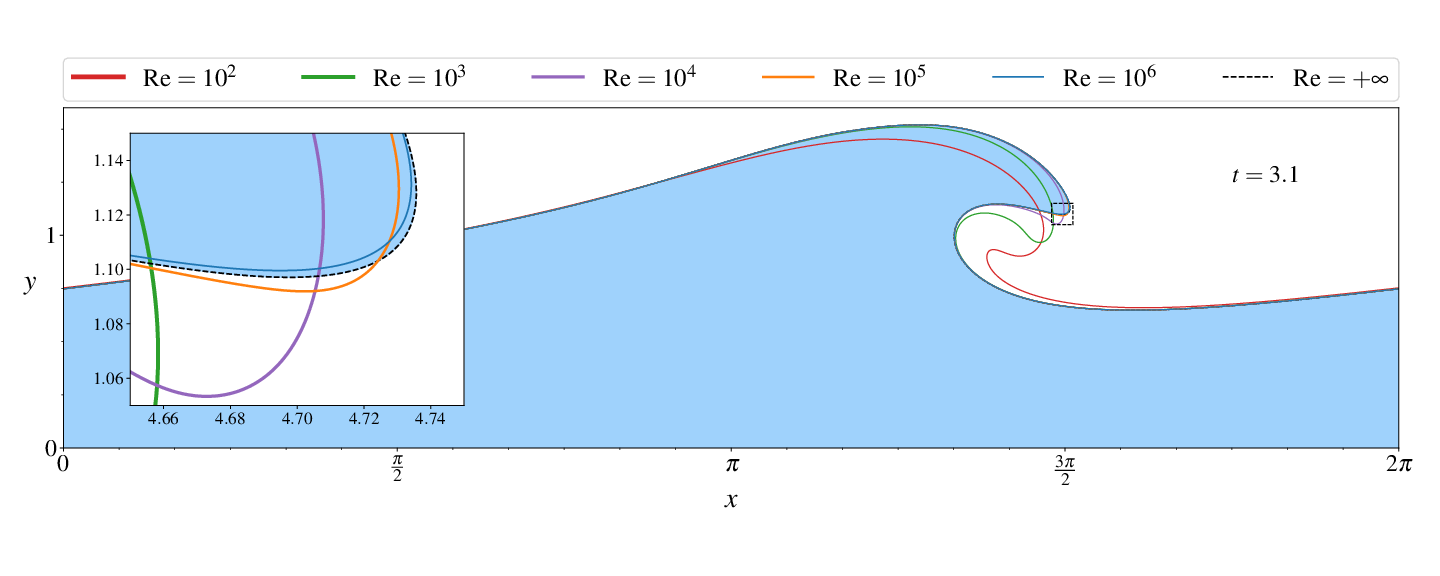
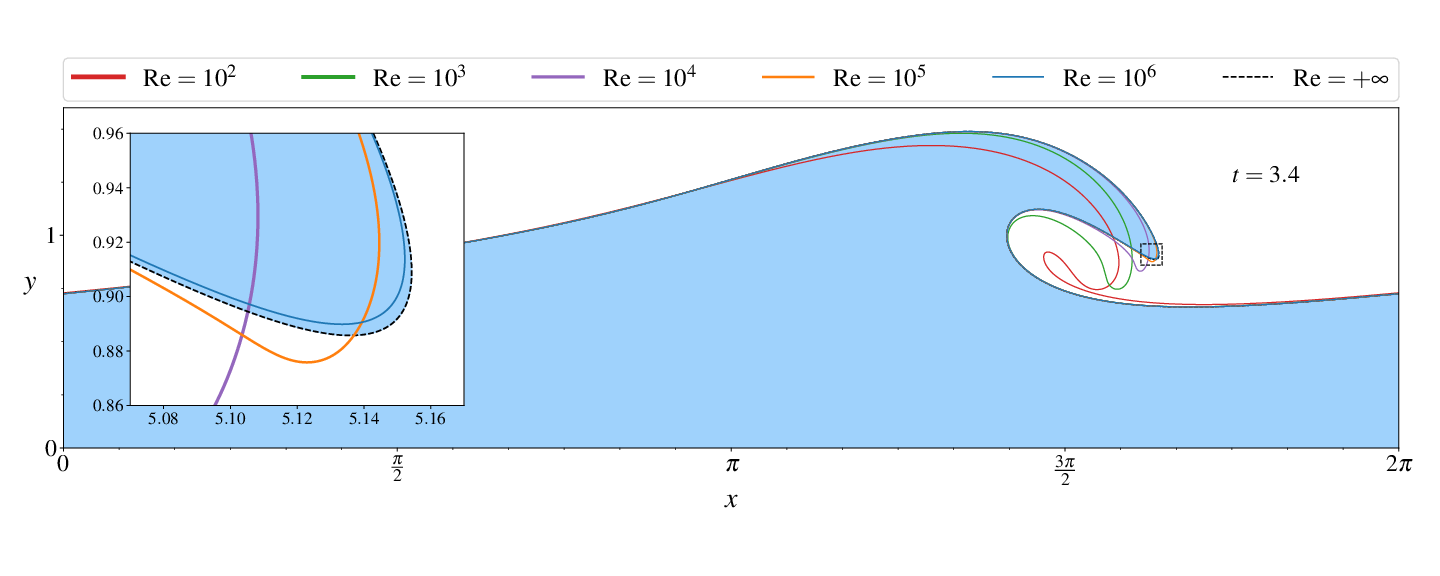
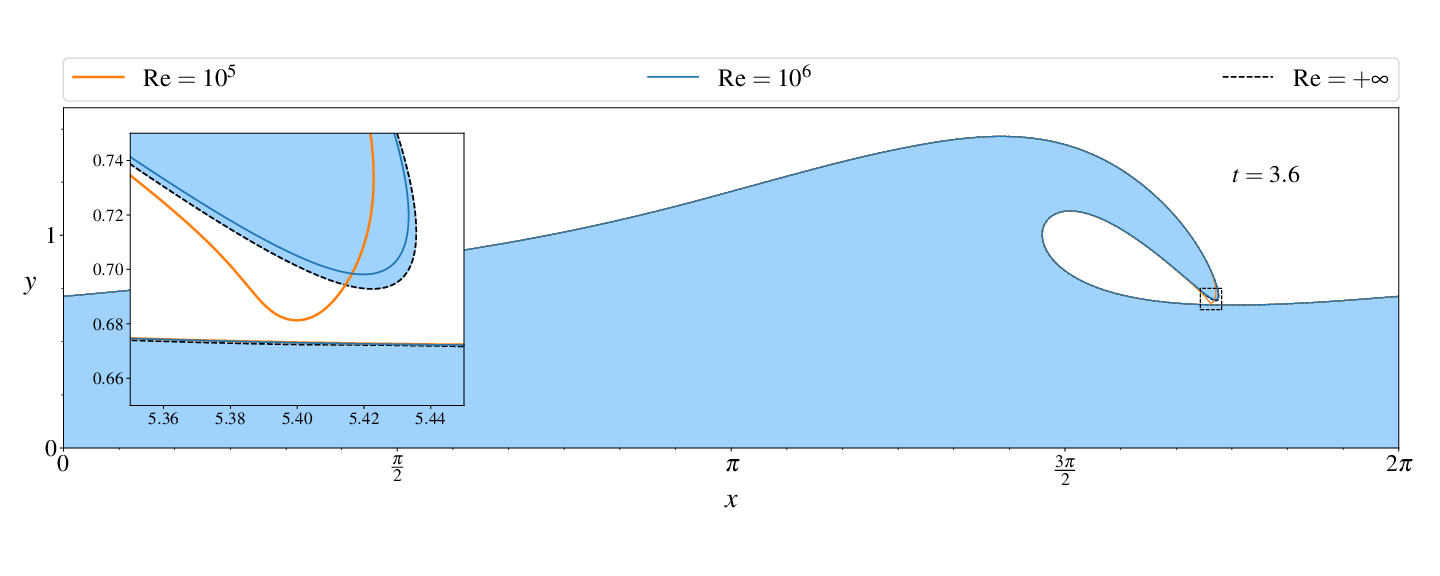
Figures (from R. & Dormy (2024)) - Convergence to the inviscid solution (computed using the numerical method of Dormy & Lacave (2024) )

A local equation for the kinetic energy can be obtained directly from the Navier-Stokes system, \[ \frac{\mathrm{D}}{\mathrm{D}t} \left( \frac{\boldsymbol{u}^2}{2} \right) = \boldsymbol{u} \cdot \boldsymbol{g} - \boldsymbol{u}\cdot \boldsymbol{\nabla} p \style{color: #42affa;}{\ - \frac{1}{\mathrm{Re}}\, \Big[ \boldsymbol{\nabla}\cdot \big( \boldsymbol{u}^{\perp} \omega \big) + \omega^2 \Big]} \] with \( \boldsymbol{u}^{\perp} = [-u_y, u_x] \). The dissipation arises in the support of the vorticity \(\omega\).

Generation of vorticity can be understood in light of the stress-free boundary condition, \[ \begin{align} p \hat{\boldsymbol{n}} - \frac{1}{\mathrm{Re}} \, \Big[ \boldsymbol{\nabla} \boldsymbol{u} + \big(\boldsymbol{\nabla}\boldsymbol{u}\big)^{\top} \Big]\, \hat{\boldsymbol{n}} = 0 \qquad & \Longrightarrow \qquad \hat{\boldsymbol{\tau}} \, \Big[ \boldsymbol{\nabla} \boldsymbol{u} + \big(\boldsymbol{\nabla}\boldsymbol{u}\big)^{\top} \Big]\, \hat{\boldsymbol{n}} = 0 \\ & \Longrightarrow \qquad \omega = 2 \kappa \big( \boldsymbol{u} \cdot \hat{\boldsymbol{\tau}} \big) - 2 \partial_s \big( \boldsymbol{u} \cdot \hat{\boldsymbol{n}} \big) \end{align} \]

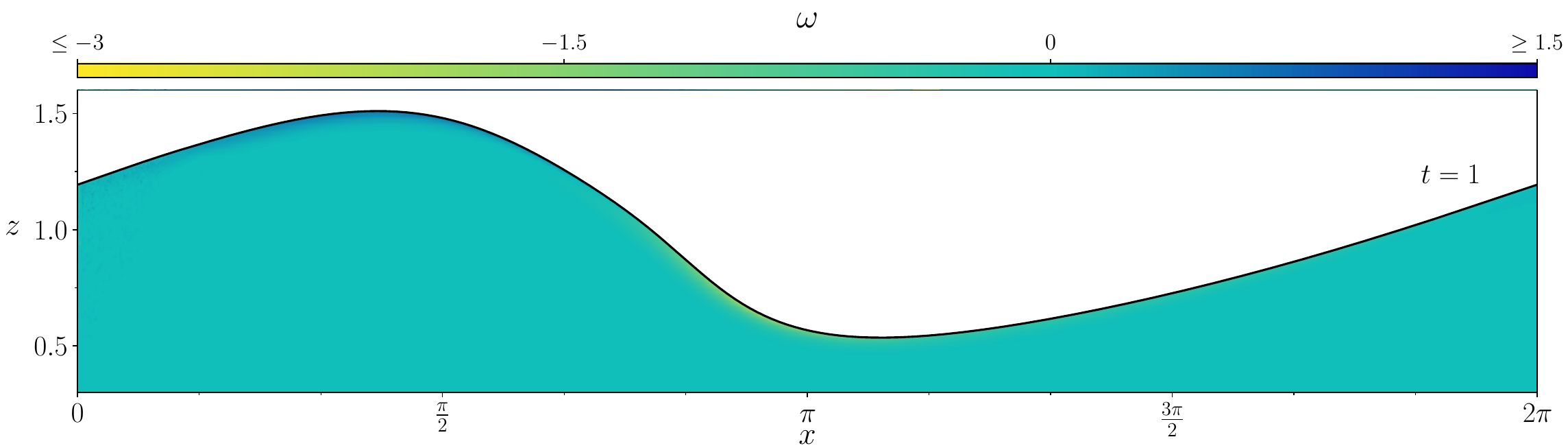
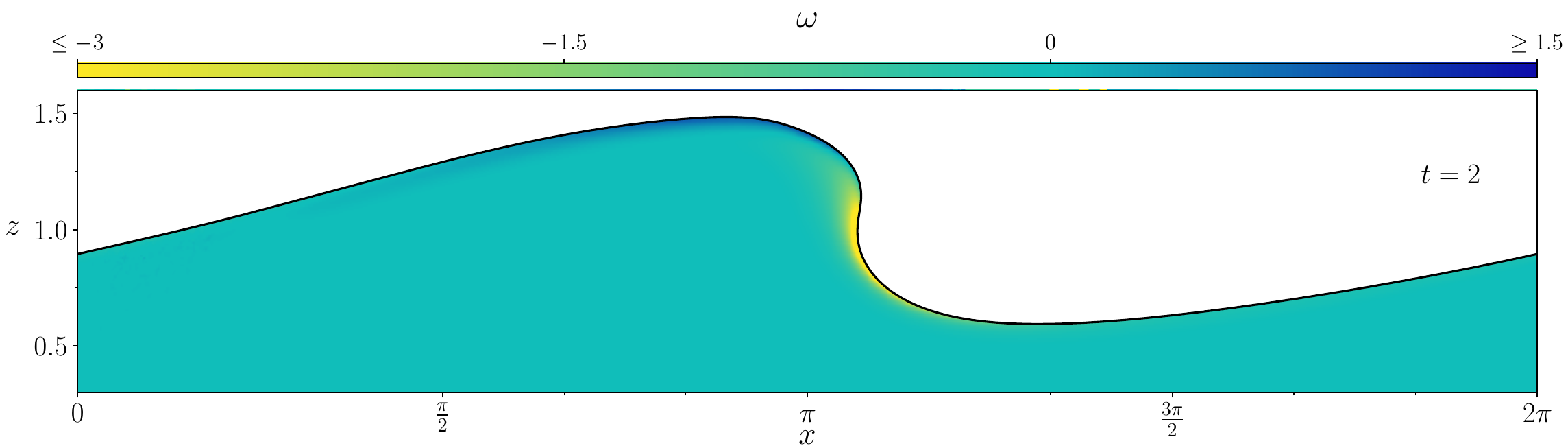
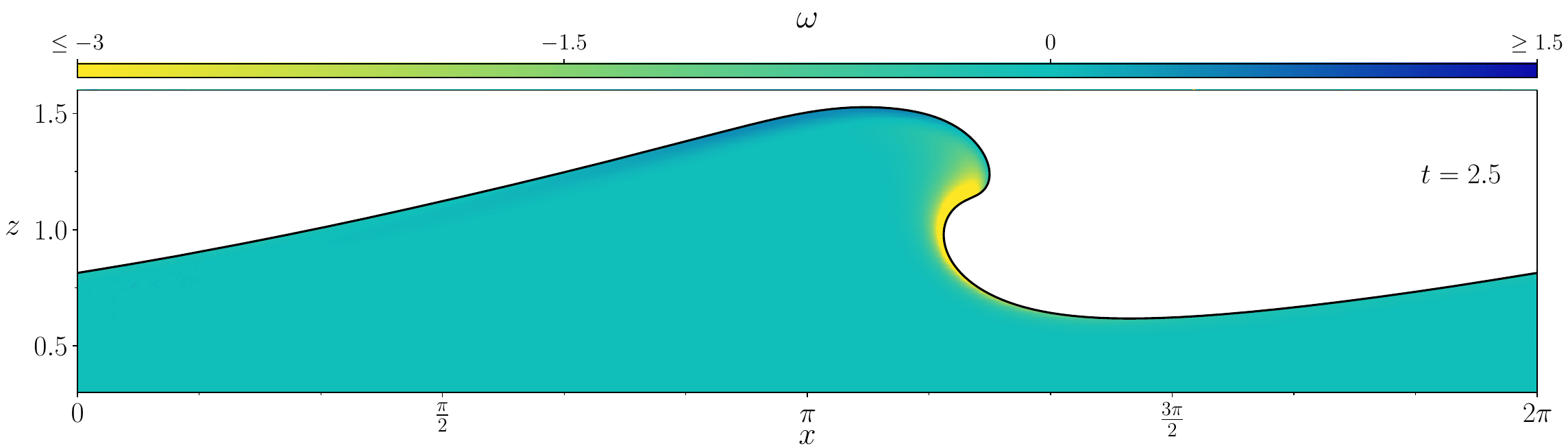
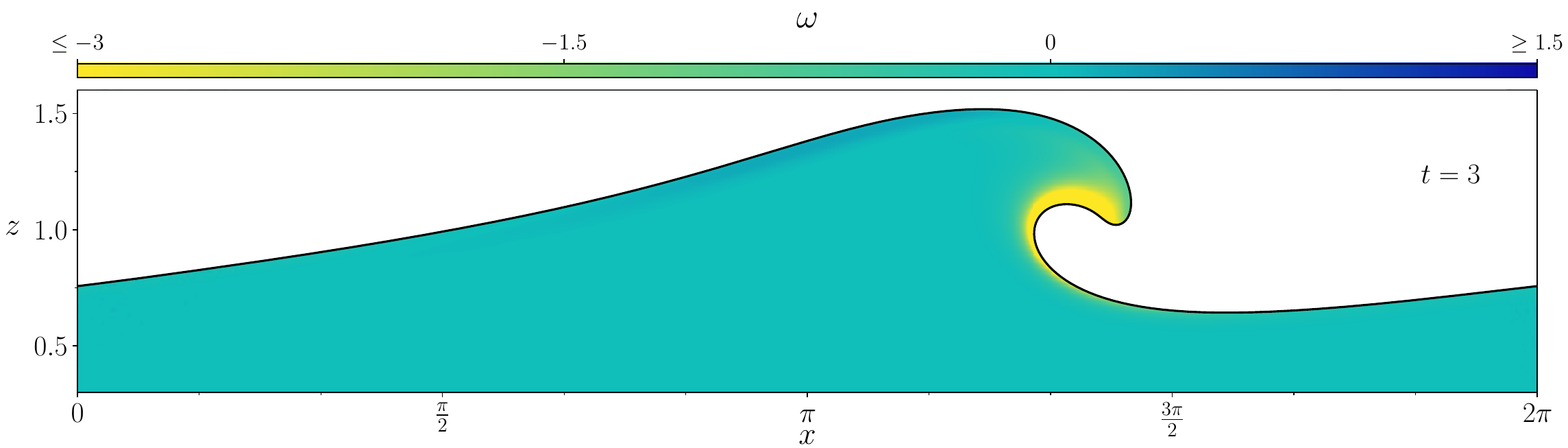
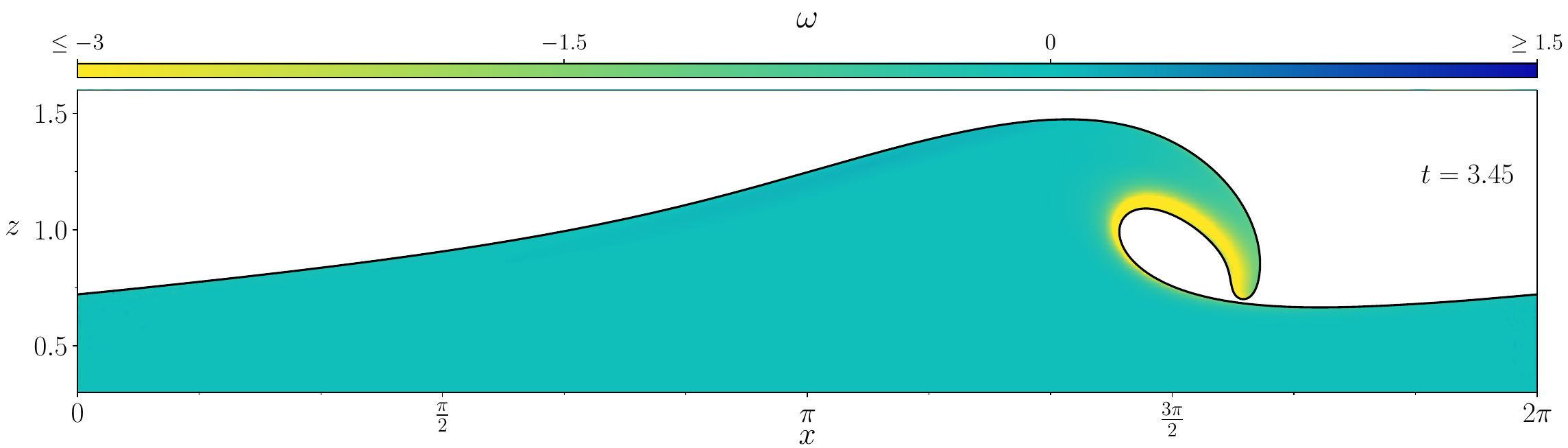
Figures (from R. & Dormy (2024)) - The vorticity generated during the \(\mathrm{Re} = 10^3\) simulation.

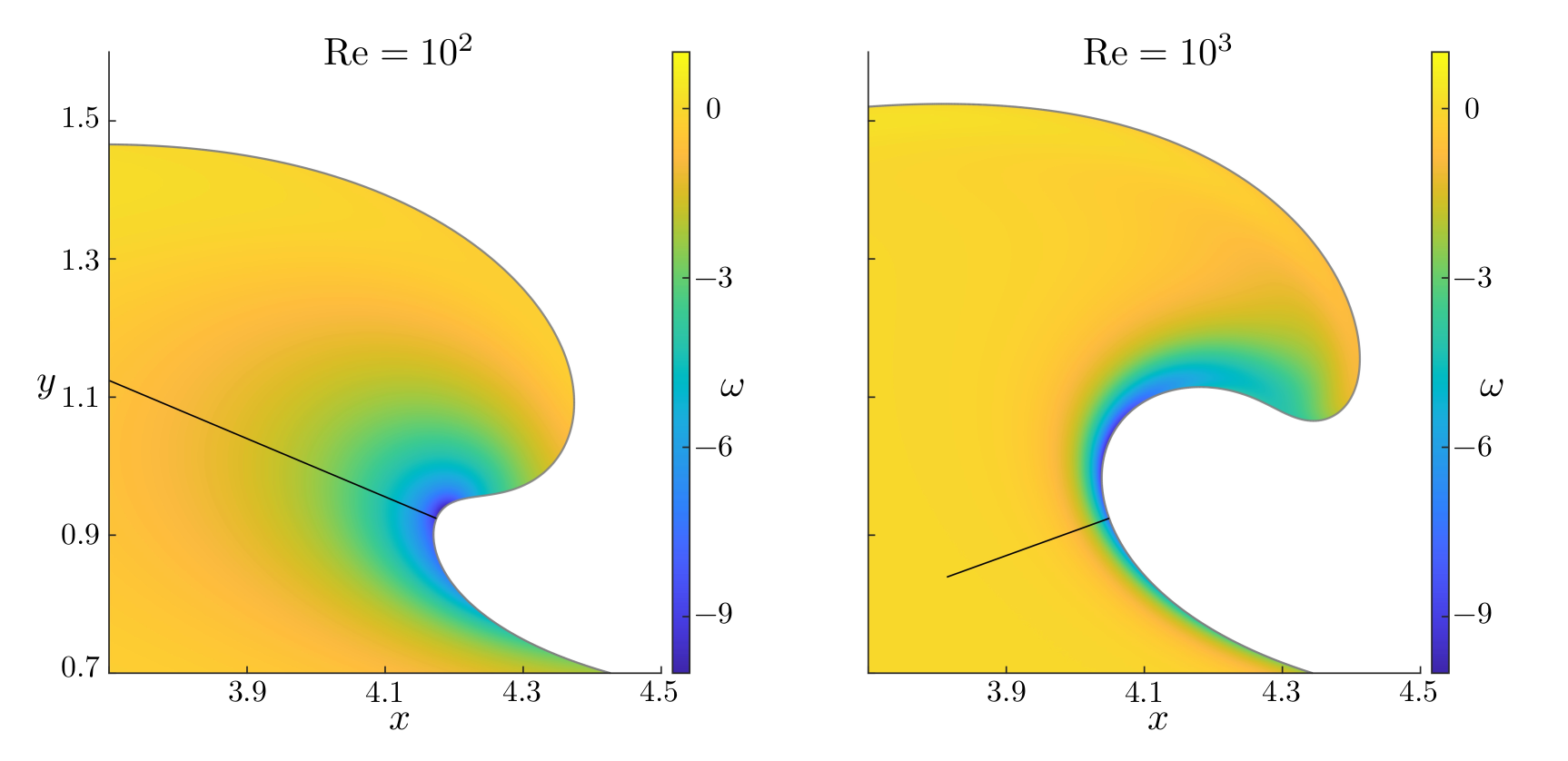
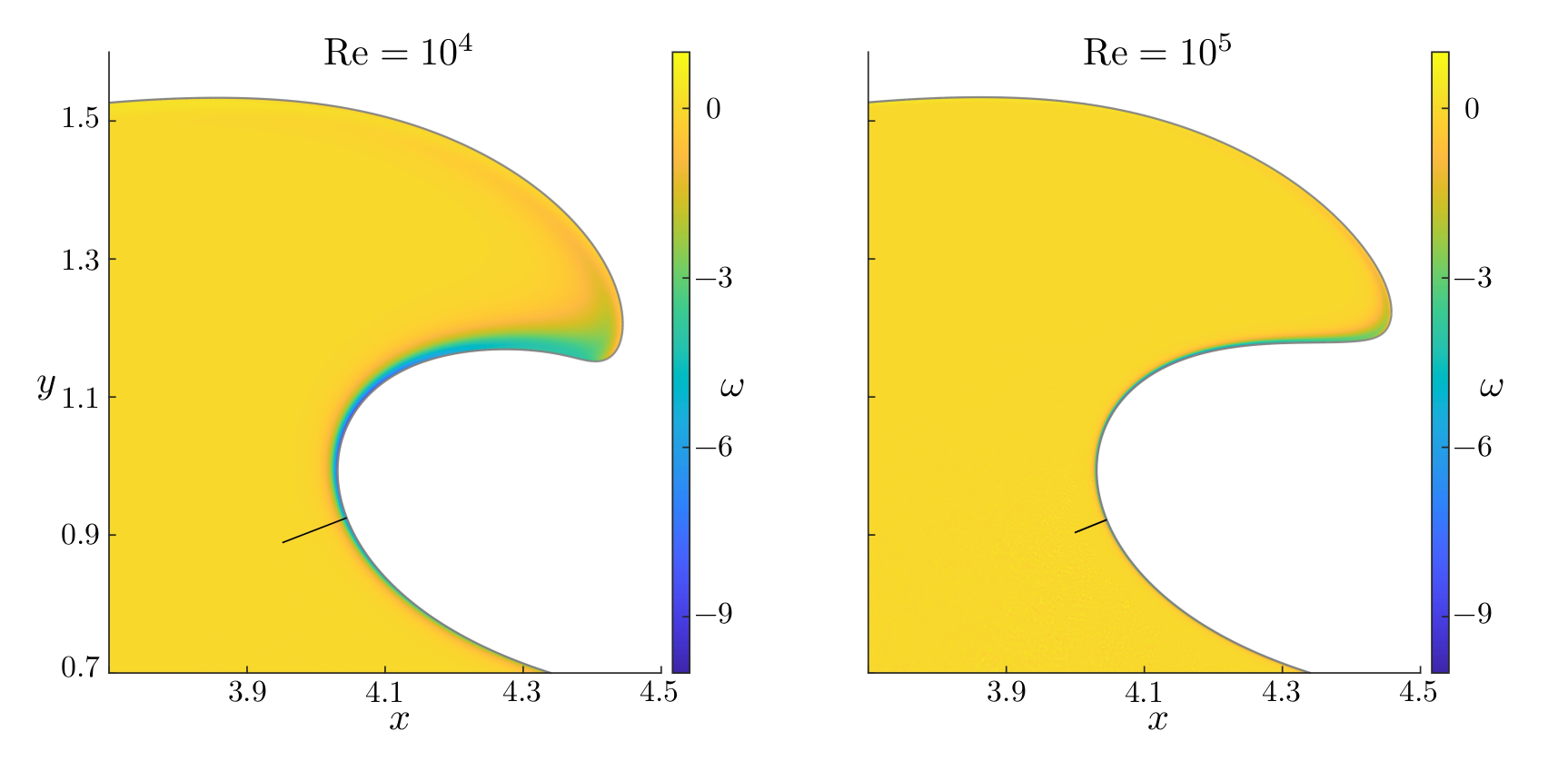
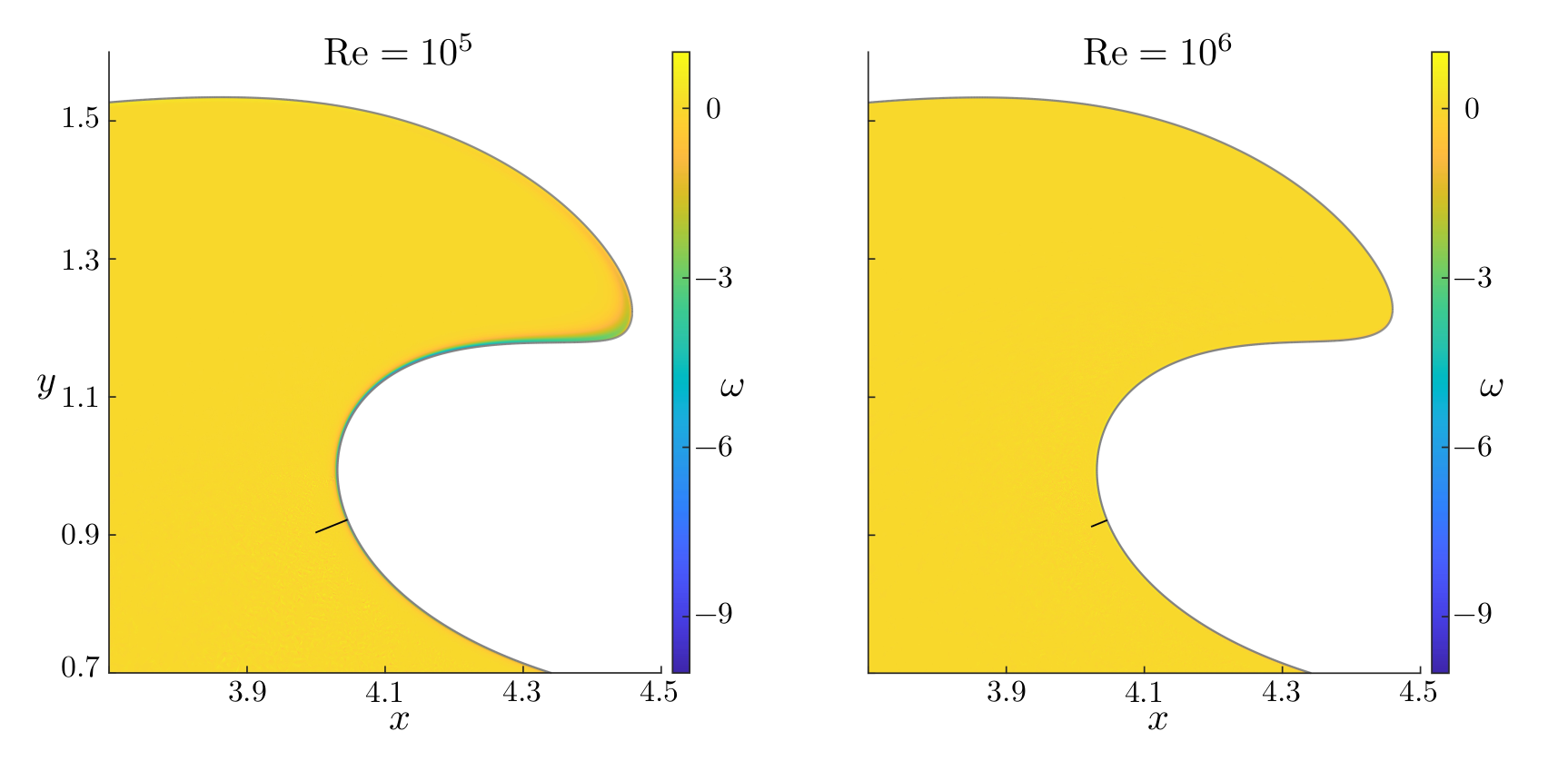
Figures (from R. & Dormy (2024)) - Close-up on the Boundary Layer at time \(t = 2.9\)

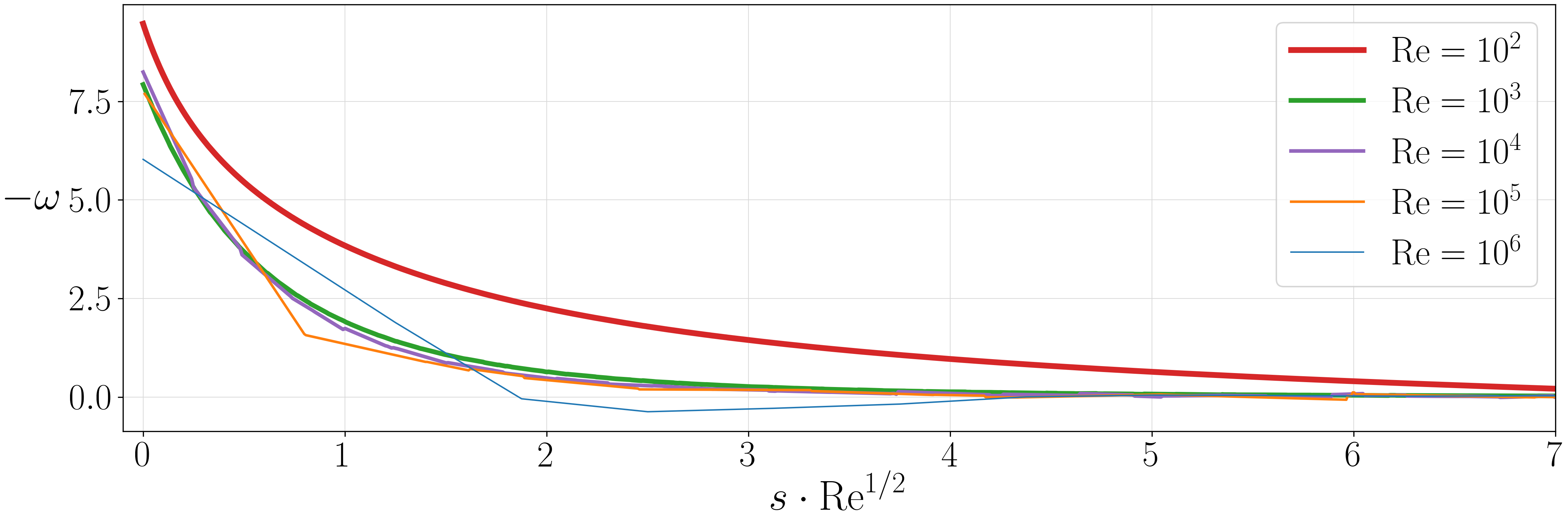
Figure (from R. & Dormy (2024)) - Corresponding vorticity cross section.

Stress-free boundary condition on the free surface \[ \begin{align} p \hat{\boldsymbol{n}} - \frac{1}{\mathrm{Re}} \, \Big[ \boldsymbol{\nabla} \boldsymbol{u} + \big(\boldsymbol{\nabla}\boldsymbol{u}\big)^{\top} \Big] \, \hat{\boldsymbol{n}} &= 0 && \text{on } \Gamma_i(t) \end{align} \] Navier No-slip/Dirichlet boundary condition on the bottom topography \(\Gamma_b\), \[ \boldsymbol{u} = 0\qquad\text{on } \Gamma_b \]

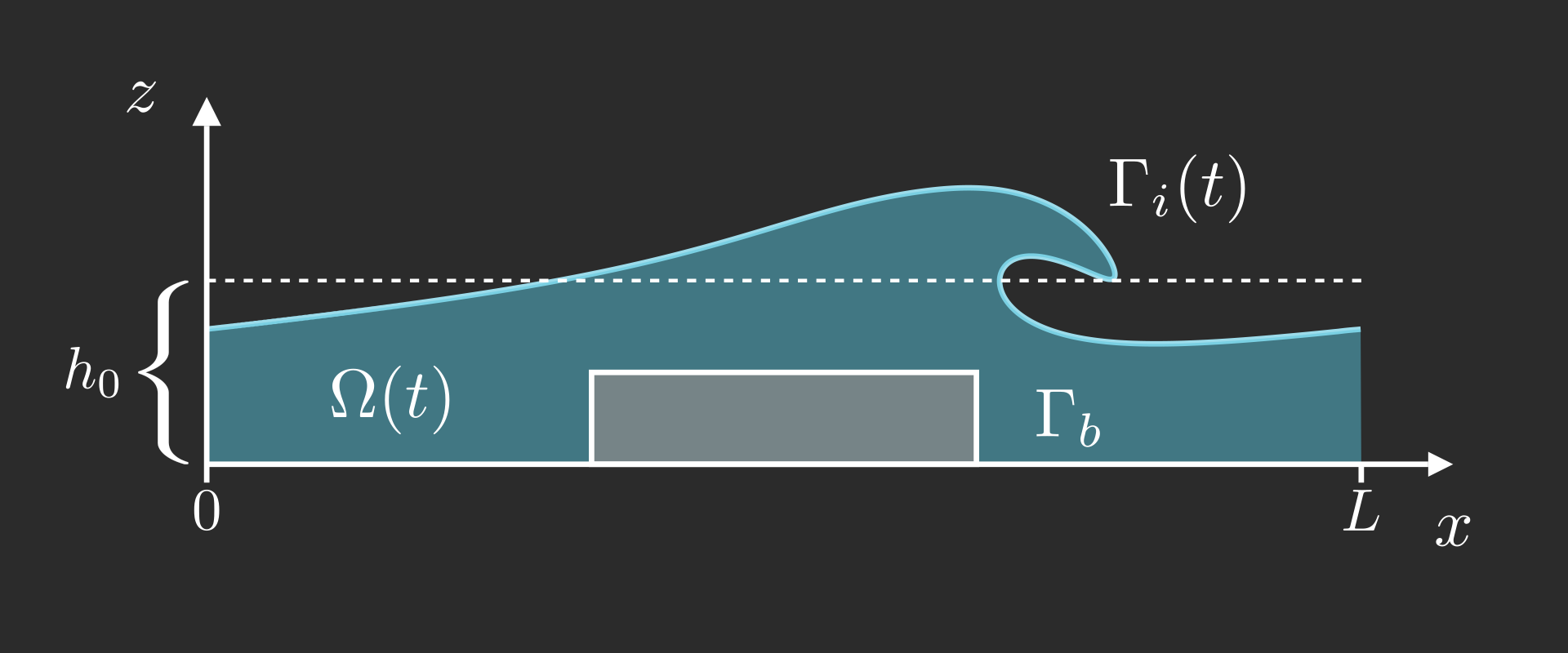
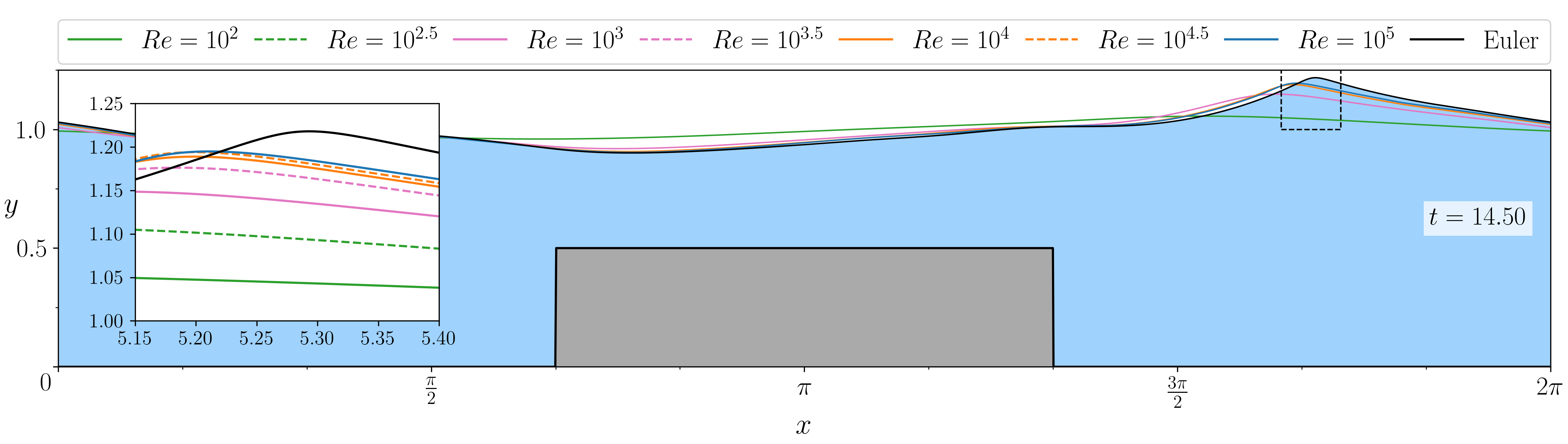
Figure (from R. & Dormy (2025, submitted)) - Comparison of the free surfaces in the case of a water wave propagating over a sharp rectangular step, for different values of Reynolds' number \(\mathrm{Re}\). The "Euler" result has been computed using the numerical method of Dormy & Lacave (2024).

We now use the no-slip/Dirichlet boundary conditions \( \boldsymbol{u} = 0 \) on \(\Gamma_b\)

Animated Figure (from R. & Dormy (2025, submitted)) - Interface evolution for a Reynolds number \(\mathrm{Re} = 10^5\), with a non-breaking water wave propagating over a sharp rectangular step.

Phenomenon already observed by Lin & Huang (2010)

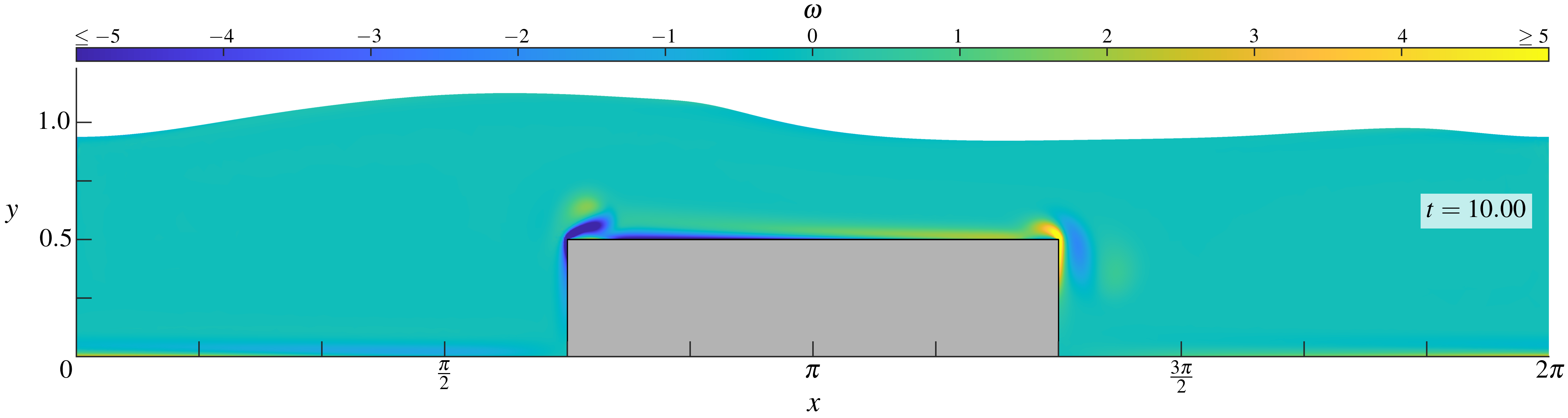
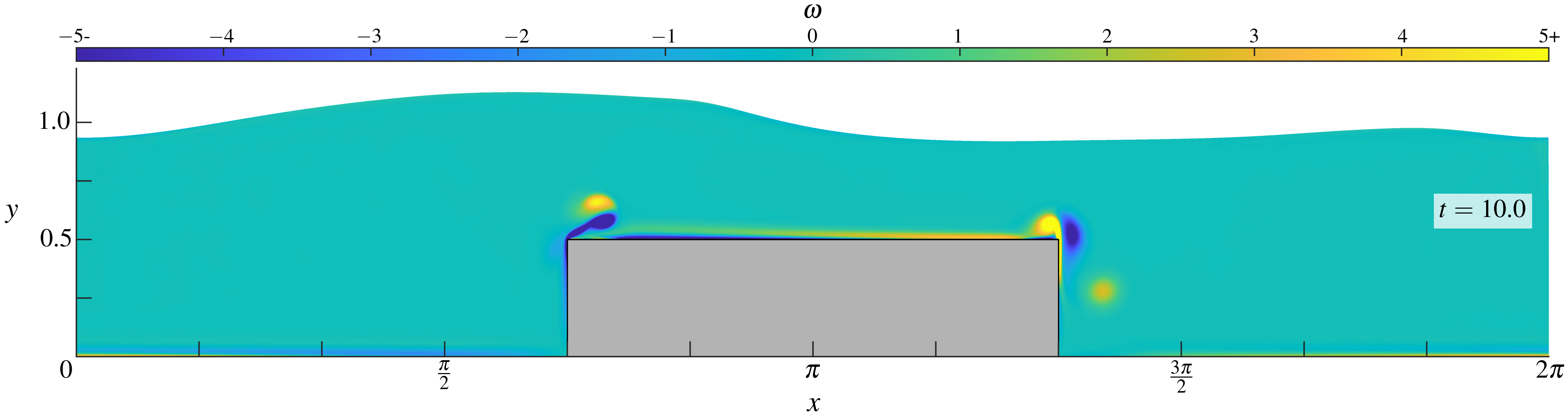
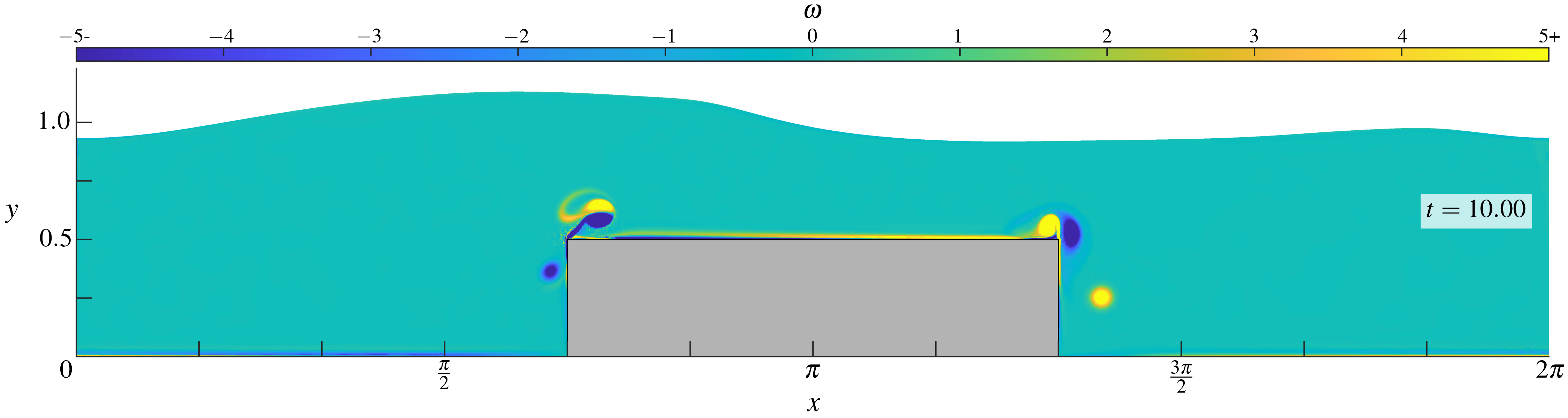
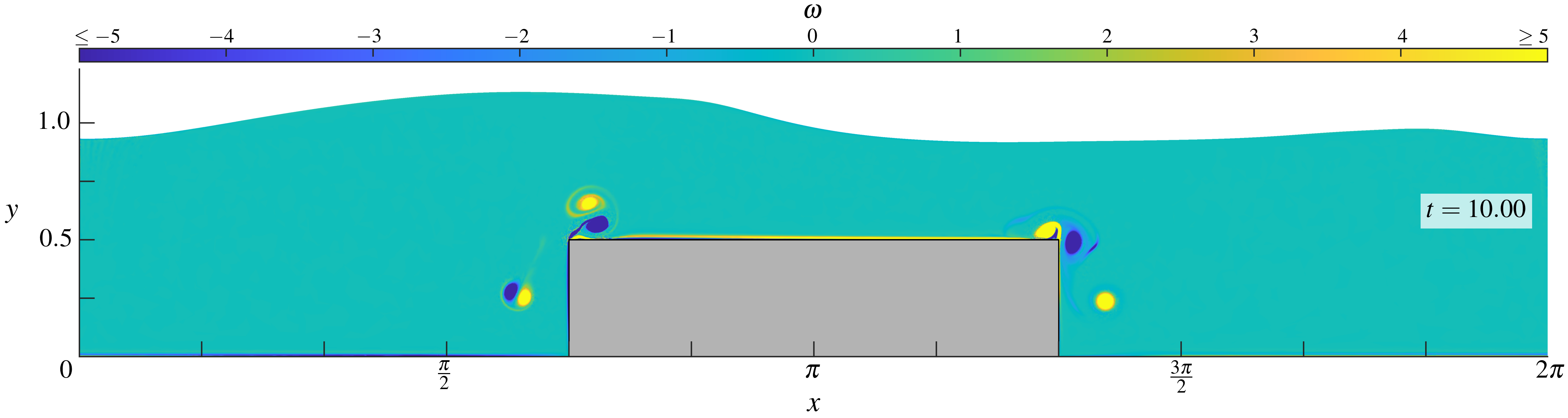
Figures (from R. & Dormy (2025, submitted)) - The vorticity at fixed time \(t = 10\) for \(\mathrm{Re} = 10^{3.5}\), \(10^4\), \(10^{4.5}\) and \(10^5\).

Figure (from R. & Dormy (2025, submitted)) - Streamlines at \(\mathrm{Re} = 10^4\) in the vicinity of the sharp rectangular step's right salient edge.

Let \(\varphi\) be the following bump function, \[ \varphi(x) = \left\{ \begin{array}{cl} \alpha \exp\left( - \frac{1}{1 - x^2} \right) & \text{for } |x| < 1 \\ 0 & \text{for } |x| \geqslant 1 \end{array} \right. \]

Let \(\varepsilon>0\) a given curvature radius. Then from the parametrisation \(\boldsymbol{\gamma}_b(s)\) of the topography \(\Gamma_b\), one can define its corresponding smooted version \(\boldsymbol{\gamma}_{b,\varepsilon}(s)\) as \[ \boldsymbol{\gamma}_{b,\varepsilon}(s) = \int_{-\varepsilon}^{\varepsilon} \boldsymbol{\gamma}_{b}(\tau - s) \cdot \frac{1}{\varepsilon} \varphi \left(\frac{\tau}{\varepsilon}\right)\, \mathrm{d}\tau \]