Non-dimensional quantities: \[ \begin{align} \boldsymbol{x} & \to h_0 \boldsymbol{x} \\ \boldsymbol{u} & \to \sqrt{gh_0} \boldsymbol{u} \\ p & \to \rho g h_0 p \\ \end{align} \] yielding the following Reynolds number, \[ \mathrm{Re} = \frac{h_0 \sqrt{gh_0}}{\nu} \]

Incompressible, non-dimensional Navier-Stokes equations in \(\Omega(t)\) \[ \begin{align} \partial_t \boldsymbol{u} + \boldsymbol{u} \cdot \boldsymbol{\nabla} \boldsymbol{u} &= - \boldsymbol{\nabla}p + \frac{1}{\mathrm{Re}}\, \Delta \boldsymbol{u} - \hat{\boldsymbol{z}} \\ \boldsymbol{\nabla} \cdot \boldsymbol{u} &= 0 \end{align} \]

Stress-free boundary condition on the free surface \[ \begin{align} p \hat{\boldsymbol{n}} - \frac{1}{\mathrm{Re}} \, \Big[ \boldsymbol{\nabla} \boldsymbol{u} + \big(\boldsymbol{\nabla}\boldsymbol{u}\big)^{\top} \Big] \, \hat{\boldsymbol{n}} &= 0 && \text{on } \Gamma_i(t) \end{align} \] Navier/free-slip boundary condition on the bottom topography \(\Gamma_b = \{z = 0\}\) \[ \begin{align} \hat{\boldsymbol{\tau}}\,\Big[\boldsymbol{\nabla} \boldsymbol{u} + \big(\boldsymbol{\nabla}\boldsymbol{u}\big)^{\top}\Big] \, \hat{\boldsymbol{n}} &= 0 & u_z &= 0 \end{align} \]

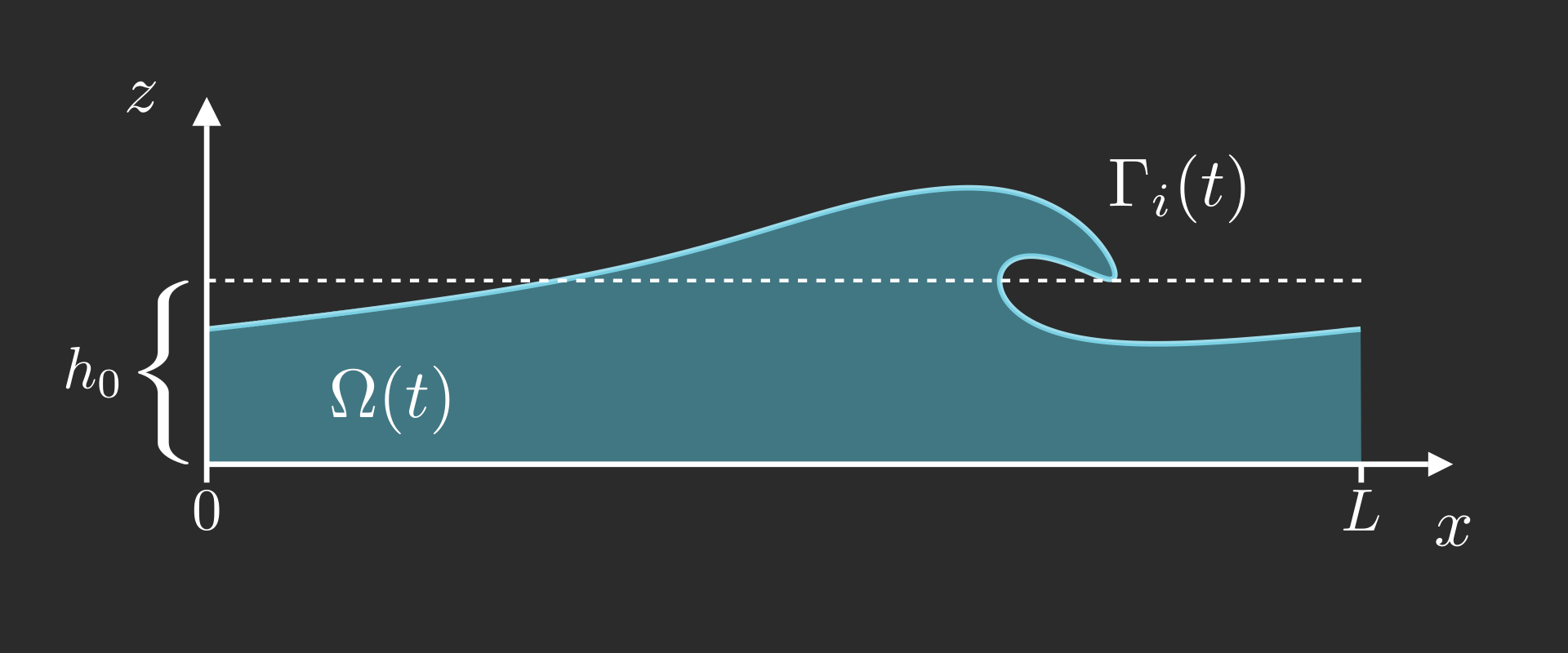
Animated Figure (from R. & Dormy (2024)) - Interface evolution for a Reynolds number \(\mathrm{Re} = 10^6\)

Figure - The mesh close to the end of the simulation shown before.

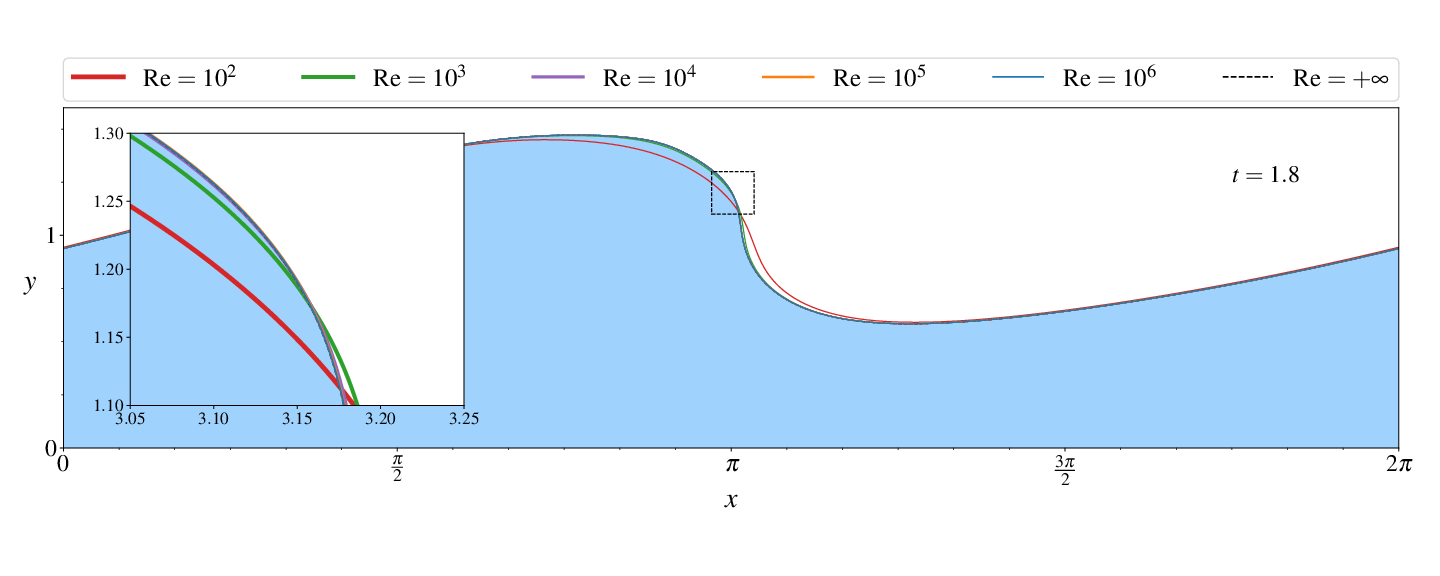
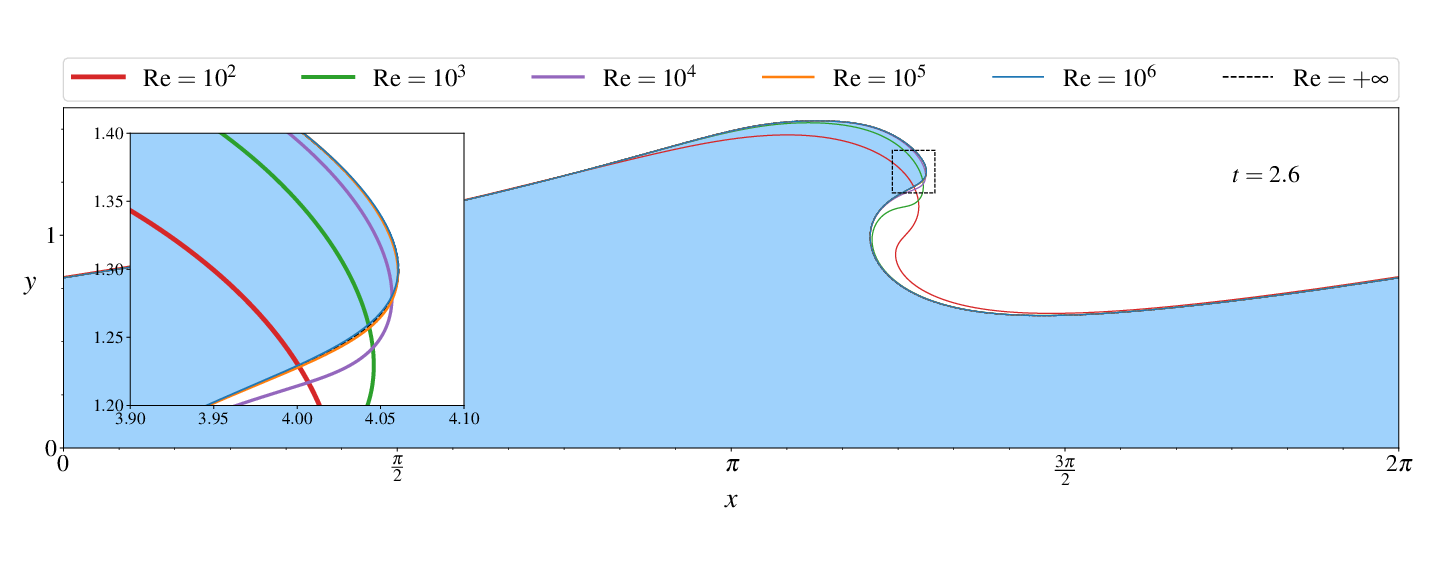
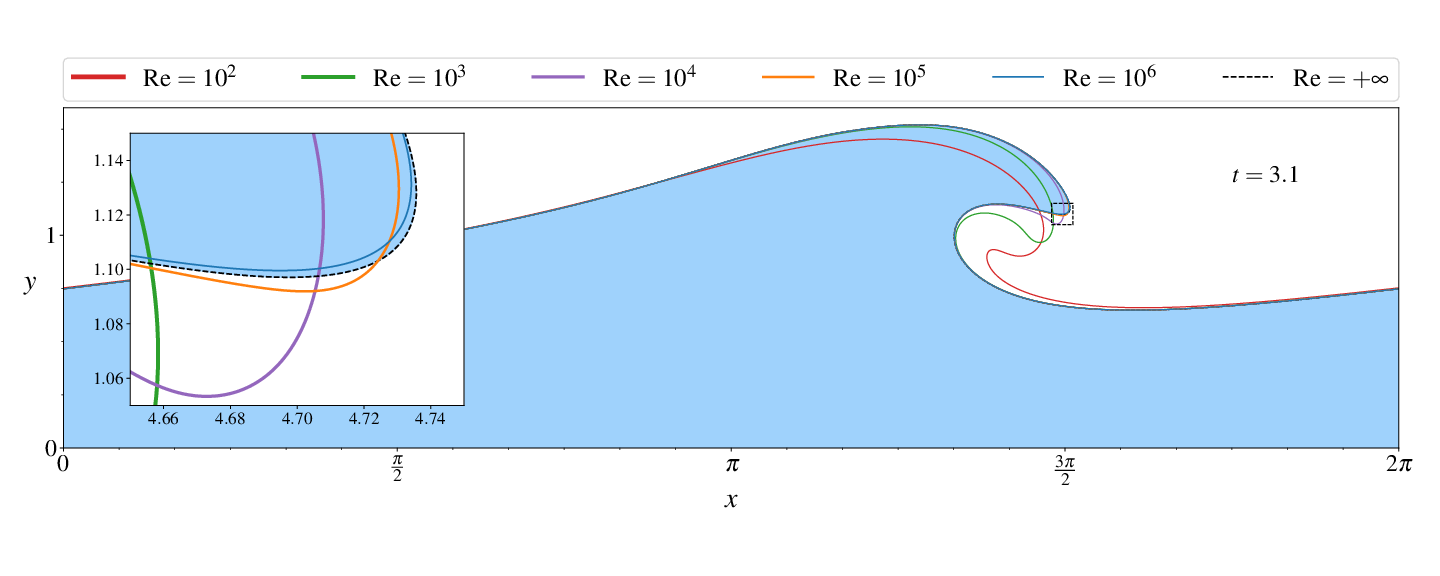
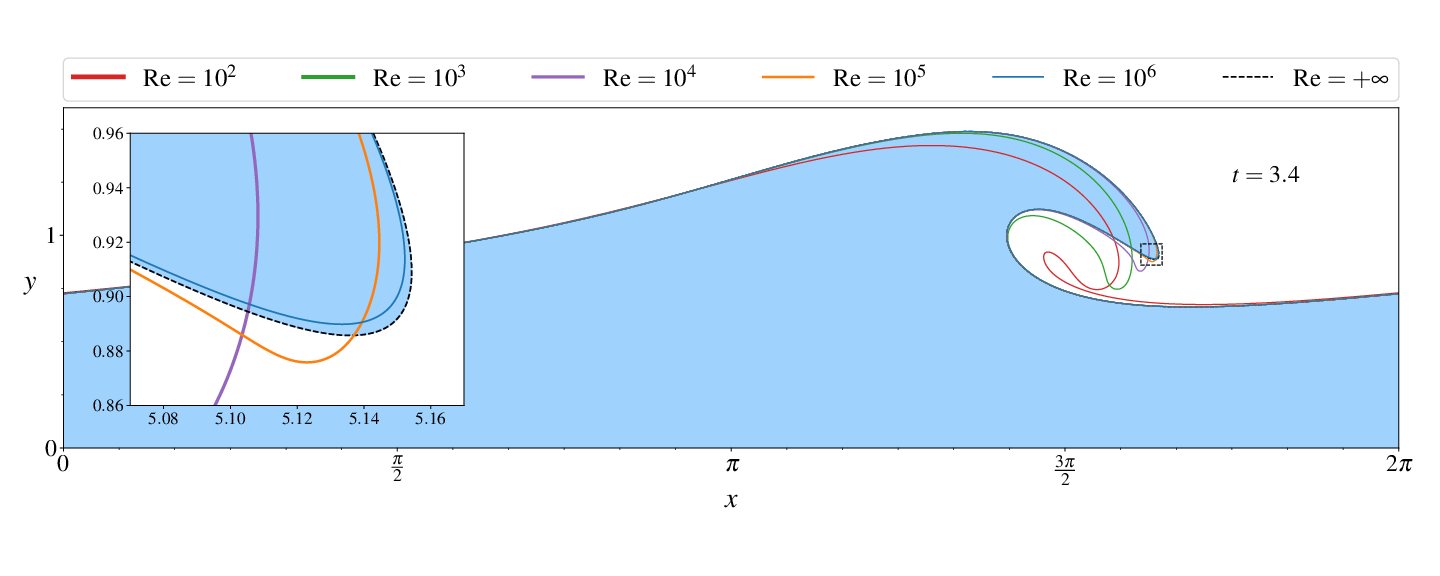
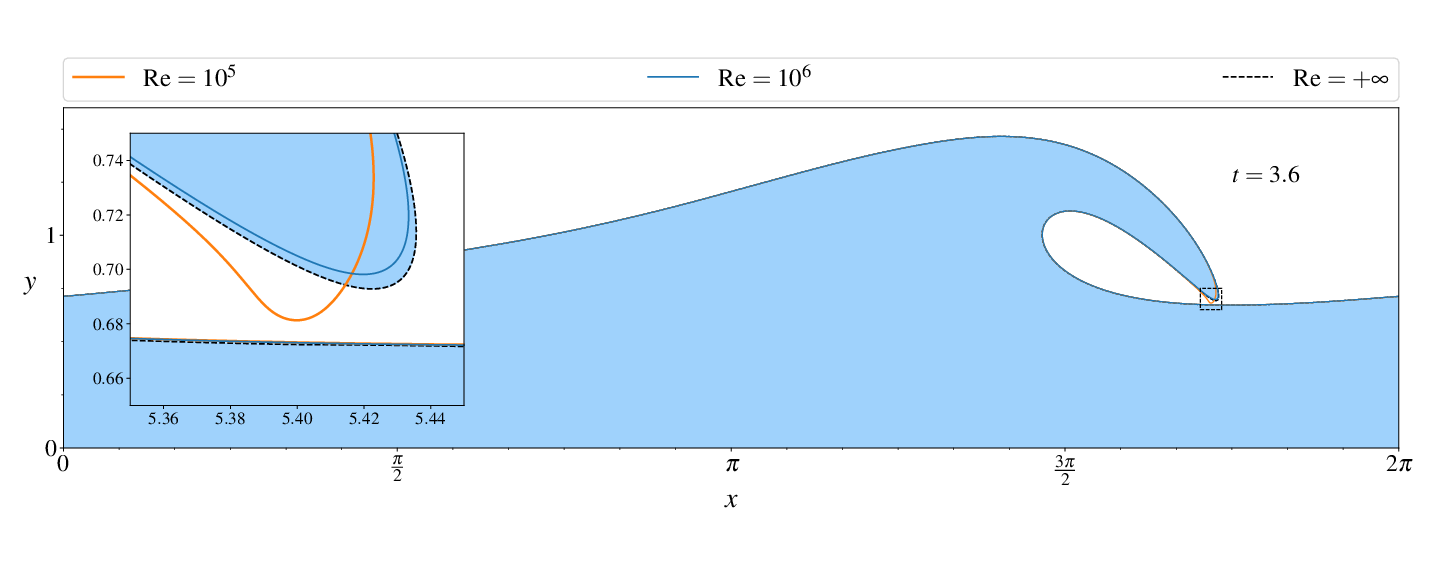
Figures (from R. & Dormy (2024)) - Convergence to the inviscid solution (computed using the numerical method of Dormy & Lacave (2024) )

A local equation for the kinetic energy can be obtained directly from the Navier-Stokes system, \[ \frac{\mathrm{D}}{\mathrm{D}t} \left( \frac{\boldsymbol{u}^2}{2} \right) = \boldsymbol{u} \cdot \boldsymbol{g} - \boldsymbol{u}\cdot \boldsymbol{\nabla} p \style{color: #42affa;}{\ - \frac{1}{\mathrm{Re}}\, \Big[ \boldsymbol{\nabla}\cdot \big( \boldsymbol{u}^{\perp} \omega \big) + \omega^2 \Big]} \] with \( \boldsymbol{u}^{\perp} = [-u_y, u_x] \). The dissipation arises in the support of the vorticity \(\omega\).

Generation of vorticity can be understood in light of the stress-free boundary condition, \[ \begin{align} p \hat{\boldsymbol{n}} - \frac{1}{\mathrm{Re}} \, \Big[ \boldsymbol{\nabla} \boldsymbol{u} + \big(\boldsymbol{\nabla}\boldsymbol{u}\big)^{\top} \Big]\, \hat{\boldsymbol{n}} = 0 \qquad & \Longrightarrow \qquad \hat{\boldsymbol{\tau}} \, \Big[ \boldsymbol{\nabla} \boldsymbol{u} + \big(\boldsymbol{\nabla}\boldsymbol{u}\big)^{\top} \Big]\, \hat{\boldsymbol{n}} = 0 \\ & \Longrightarrow \qquad \omega = 2 \kappa \big( \boldsymbol{u} \cdot \hat{\boldsymbol{\tau}} \big) - 2 \partial_s \big( \boldsymbol{u} \cdot \hat{\boldsymbol{n}} \big) \end{align} \]

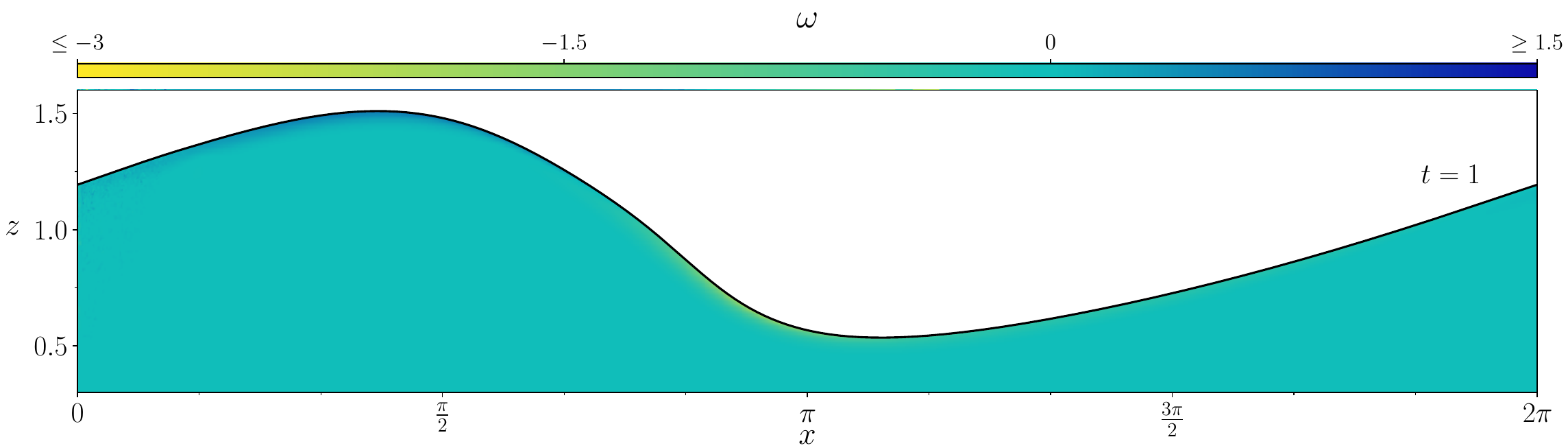
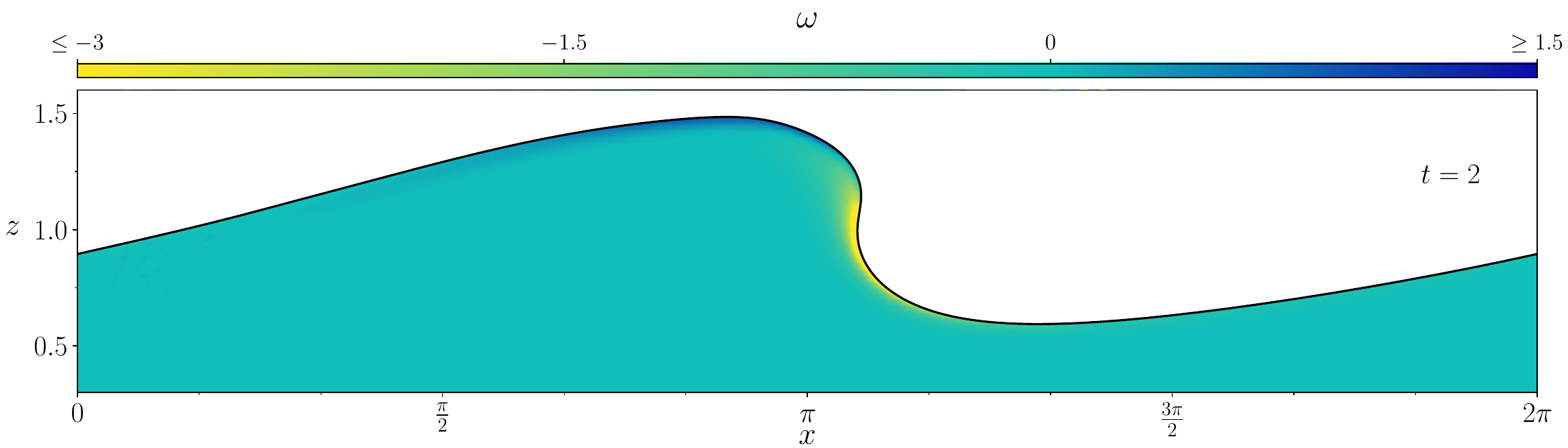
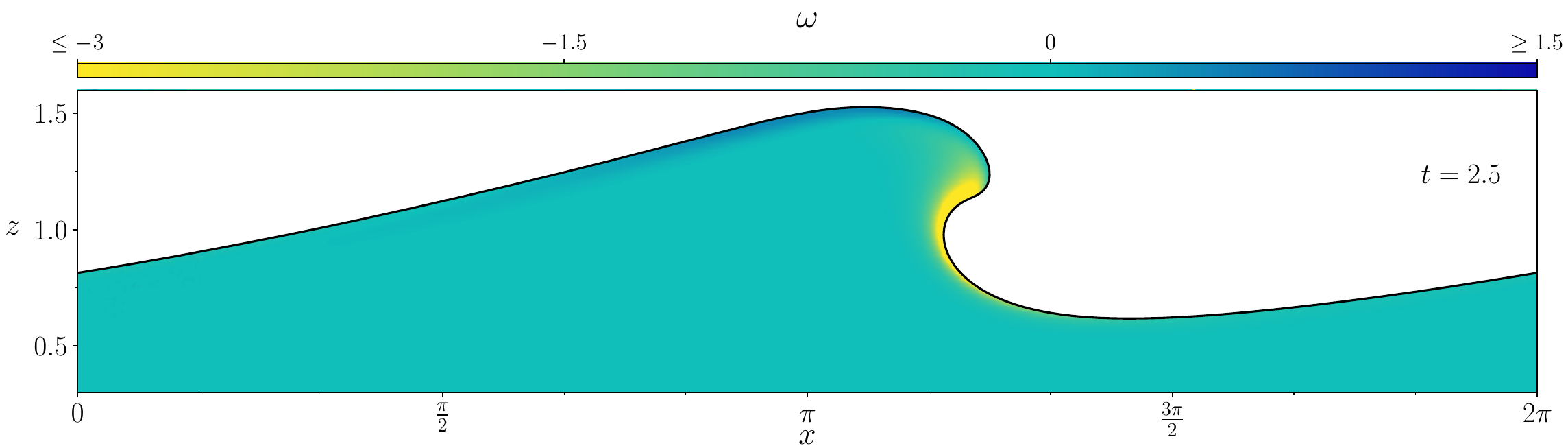
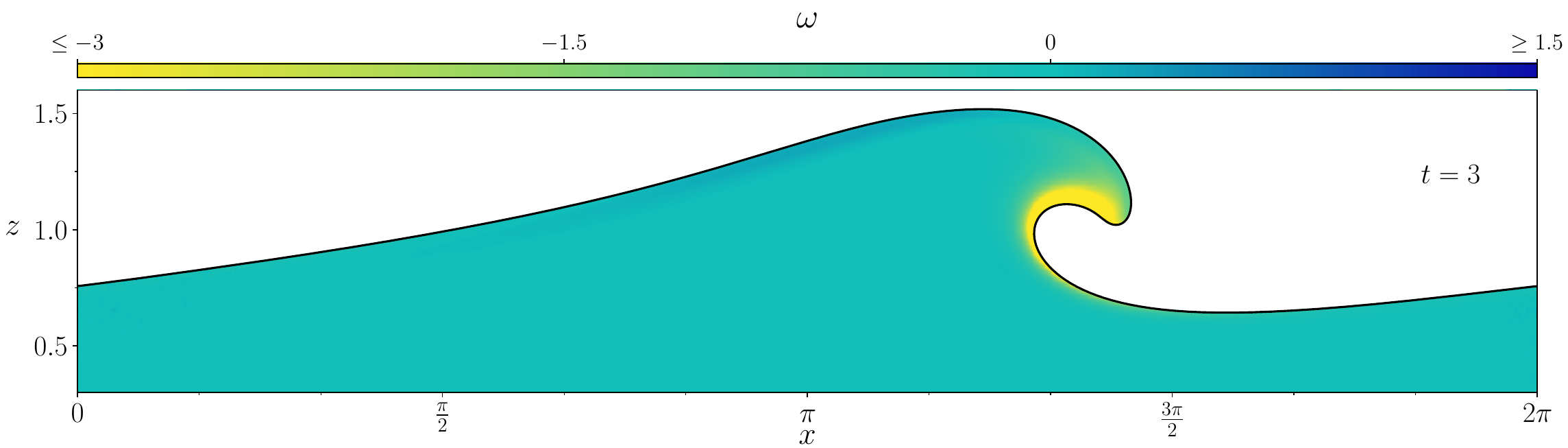
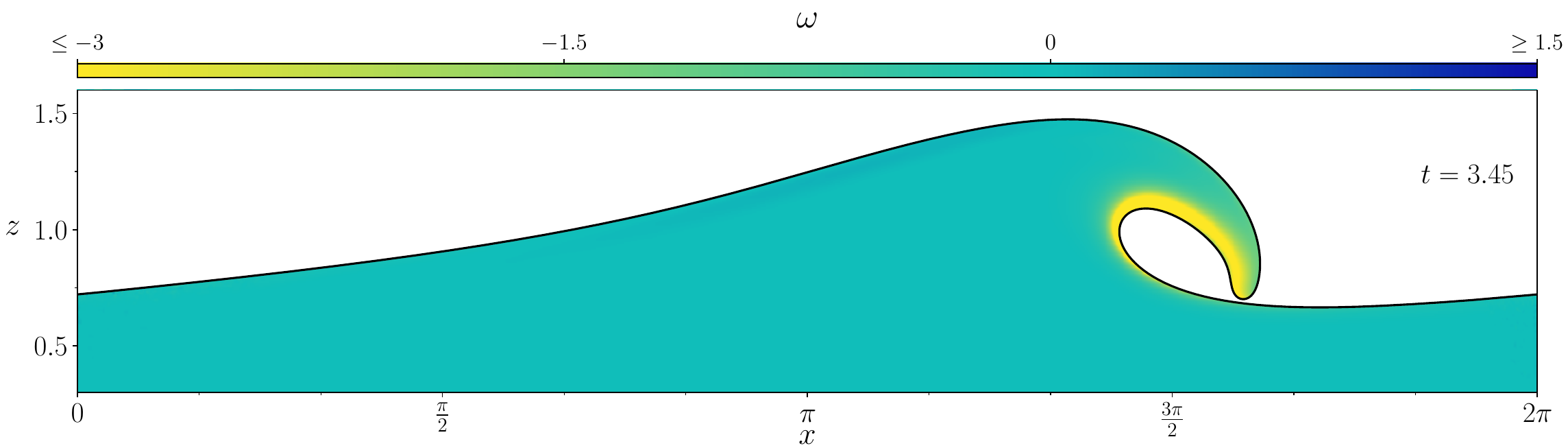
Figures (from R. & Dormy (2024)) - The vorticity generated during the \(\mathrm{Re} = 10^3\) simulation.

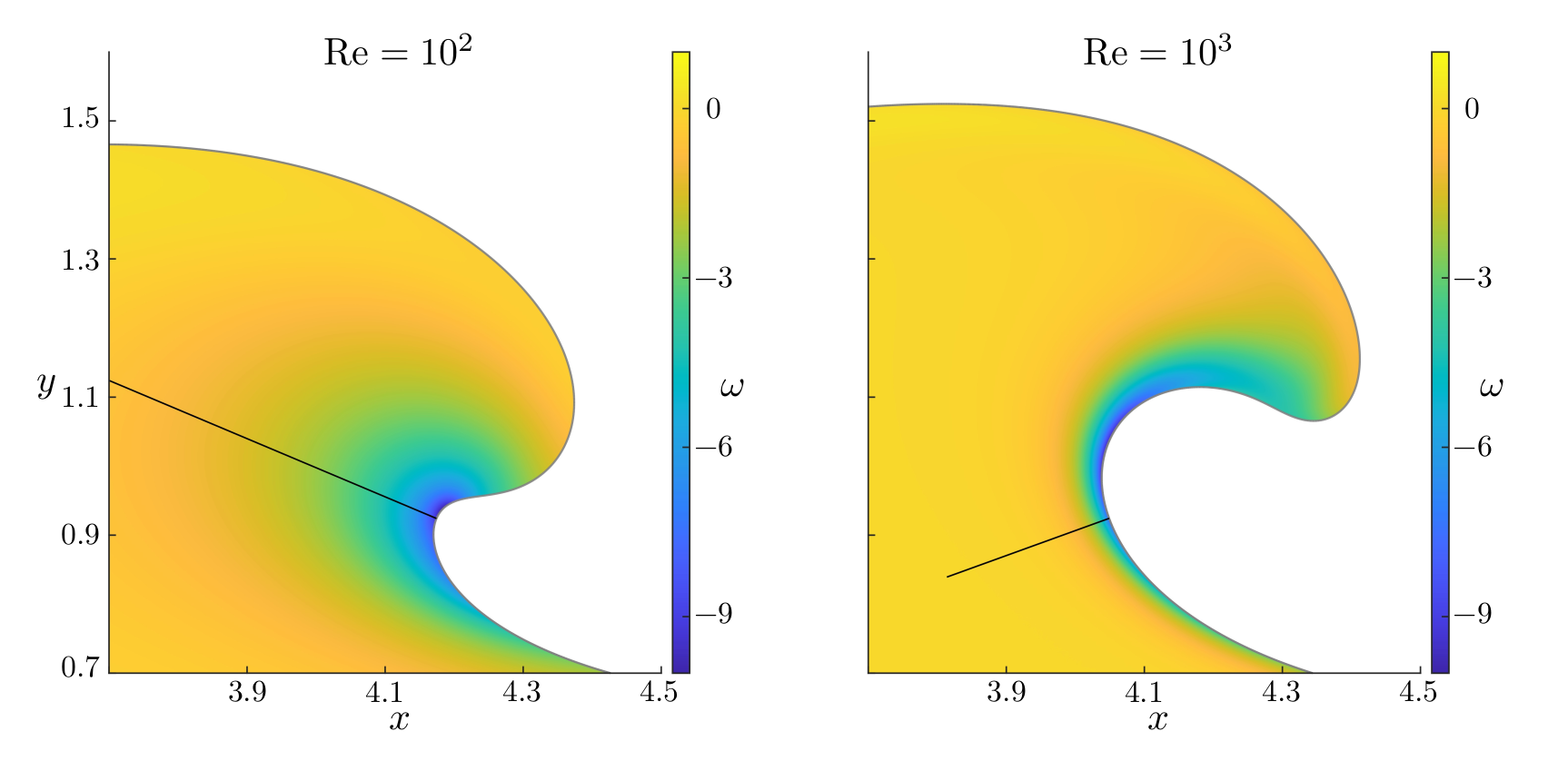
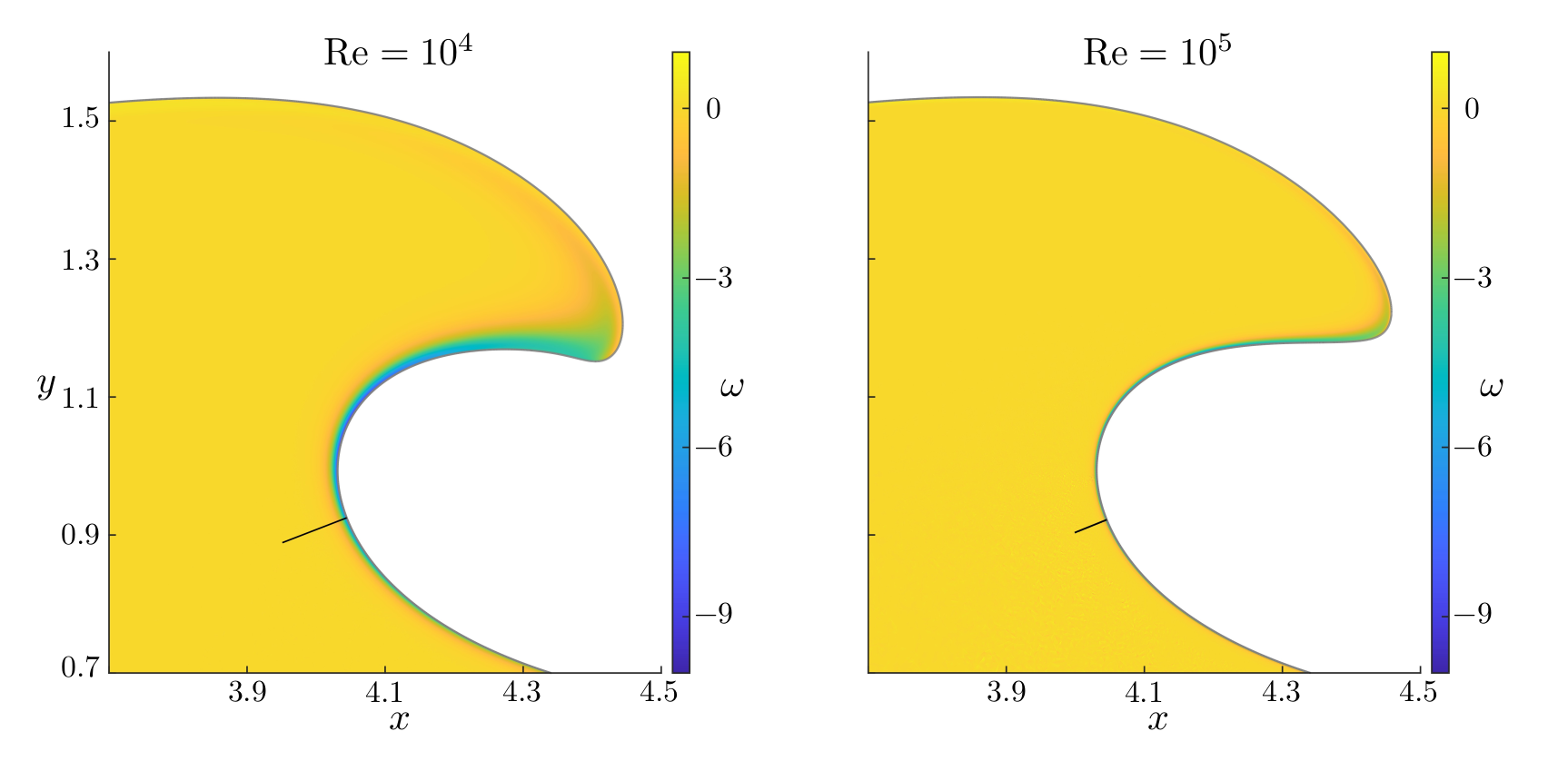
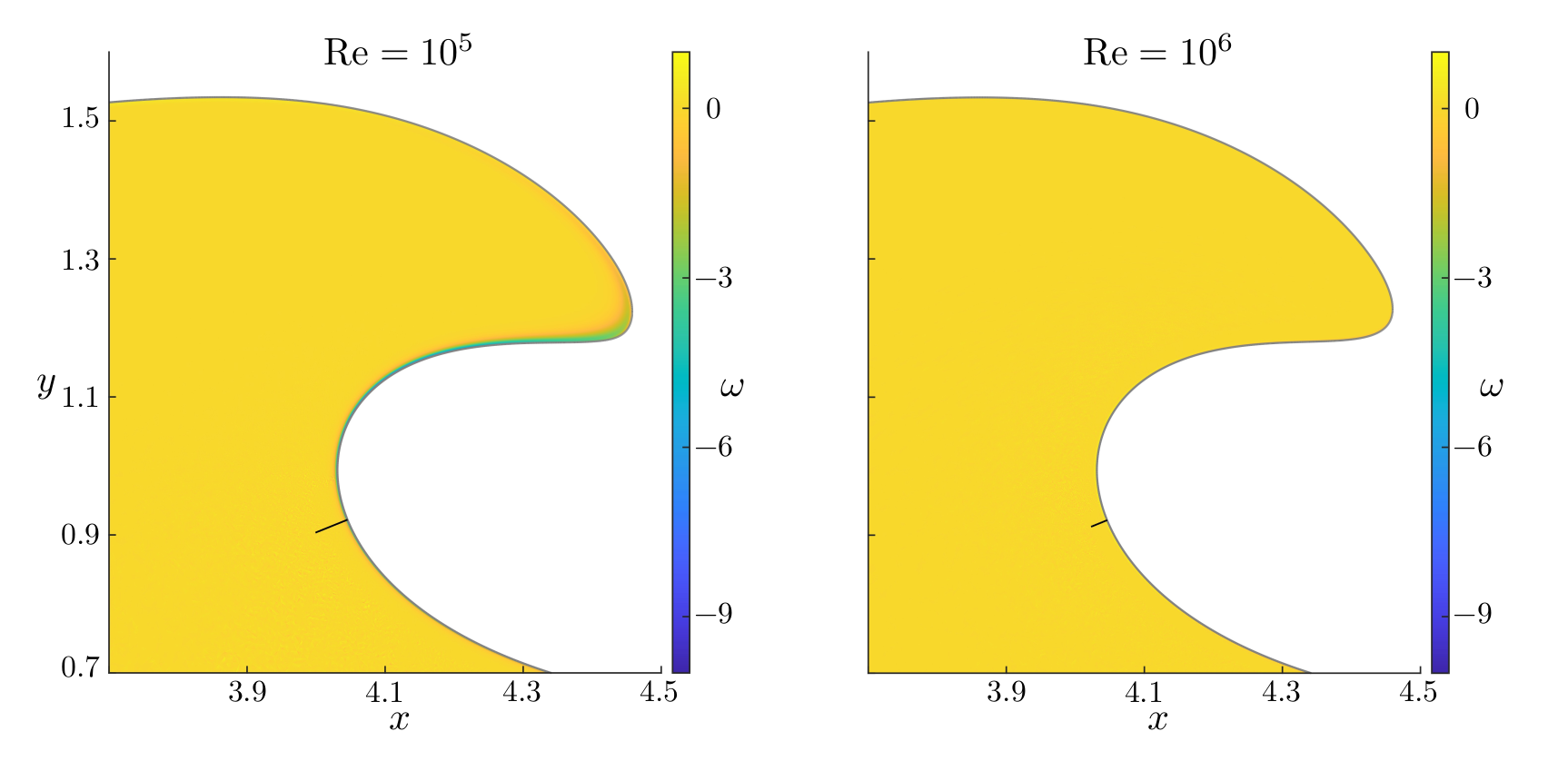
Figures (from R. & Dormy (2024)) - Close-up on the Boundary Layer at time \(t = 2.9\)

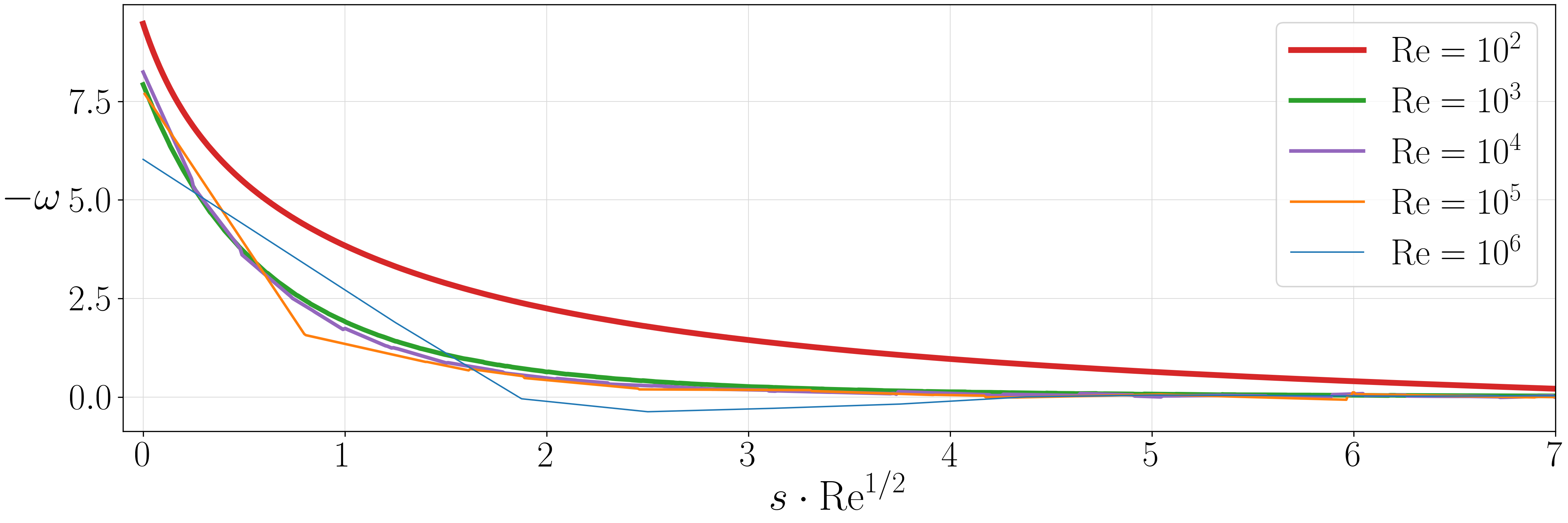
Figure (from R. & Dormy (2024)) - Corresponding vorticity cross section.

Stress-free boundary condition on the free surface \[ \begin{align} p \hat{\boldsymbol{n}} - \frac{1}{\mathrm{Re}} \, \Big[ \boldsymbol{\nabla} \boldsymbol{u} + \big(\boldsymbol{\nabla}\boldsymbol{u}\big)^{\top} \Big] \, \hat{\boldsymbol{n}} &= 0 && \text{on } \Gamma_i(t) \end{align} \] Navier/free-slip No-slip/Dirichlet boundary condition on the bottom topography \(\Gamma_b\), \[ \boldsymbol{u} = 0\qquad\text{on } \Gamma_b \]

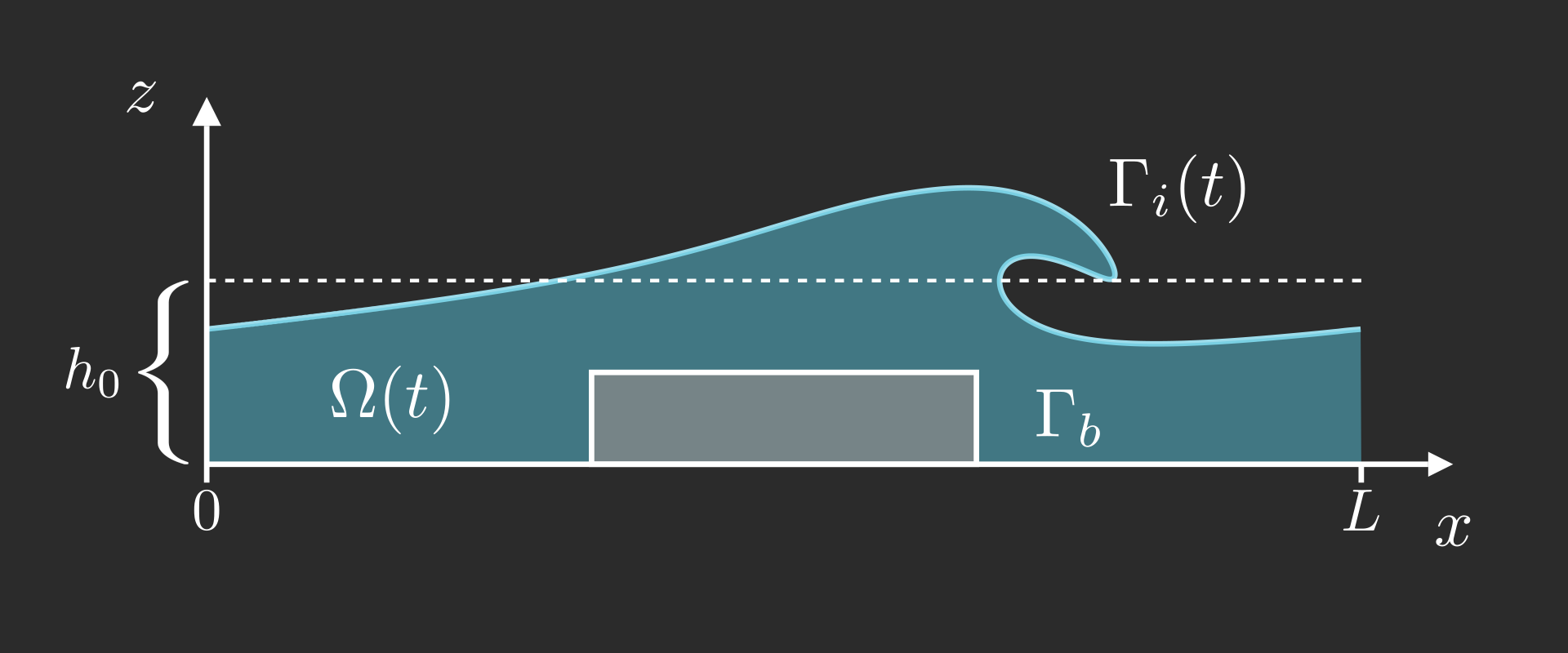
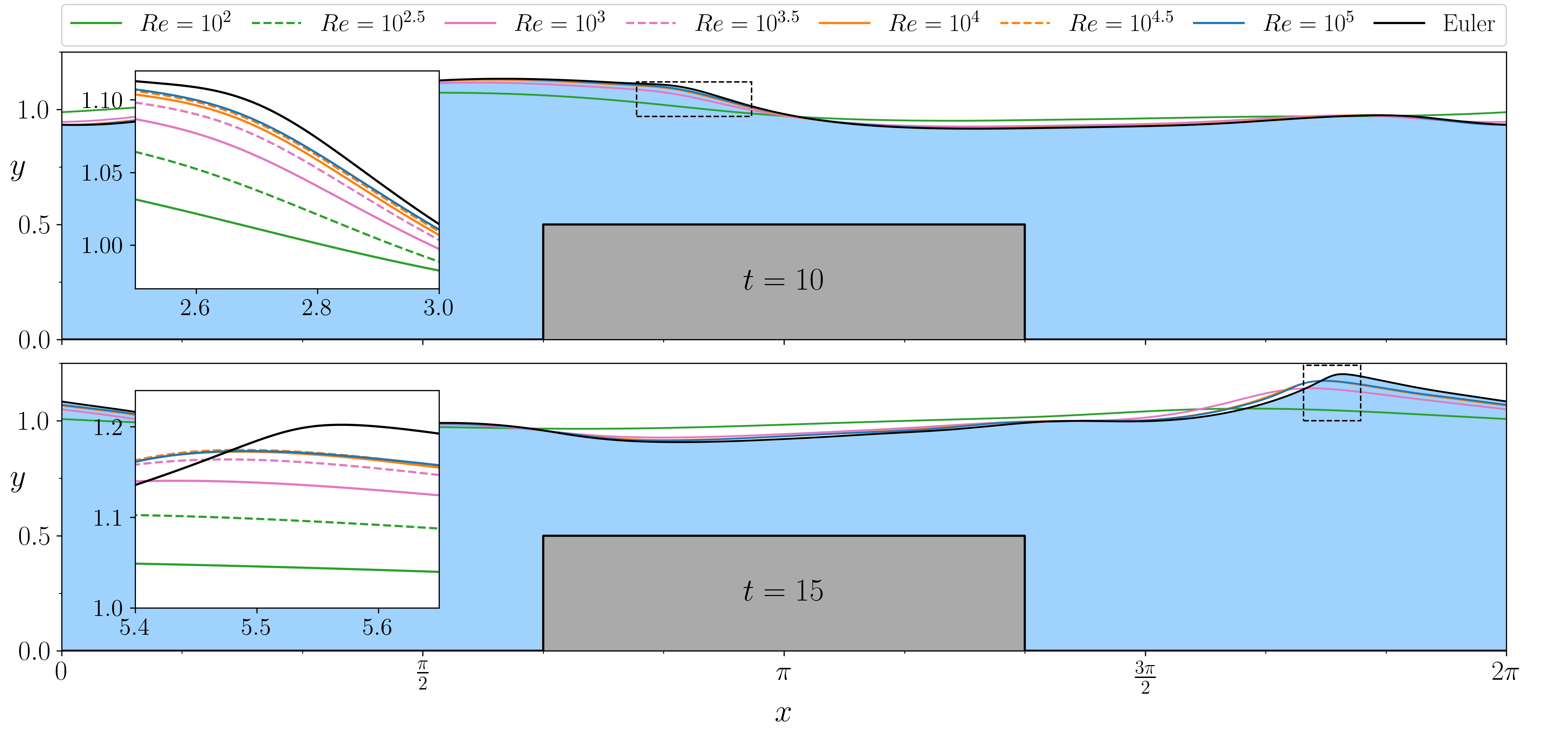
Figure (from R. & Dormy (2025, in press)) - Free surfaces for different values of Reynolds' number \(\mathrm{Re}\). The "Euler" result has been computed using the numerical method of Dormy & Lacave (2024).

Animated Figure (from R. & Dormy (2025, in press)) - Vorticity evolution for a Reynolds number \(\mathrm{Re} = 10^5\).

Phenomenon already observed by Lin & Huang (2010)

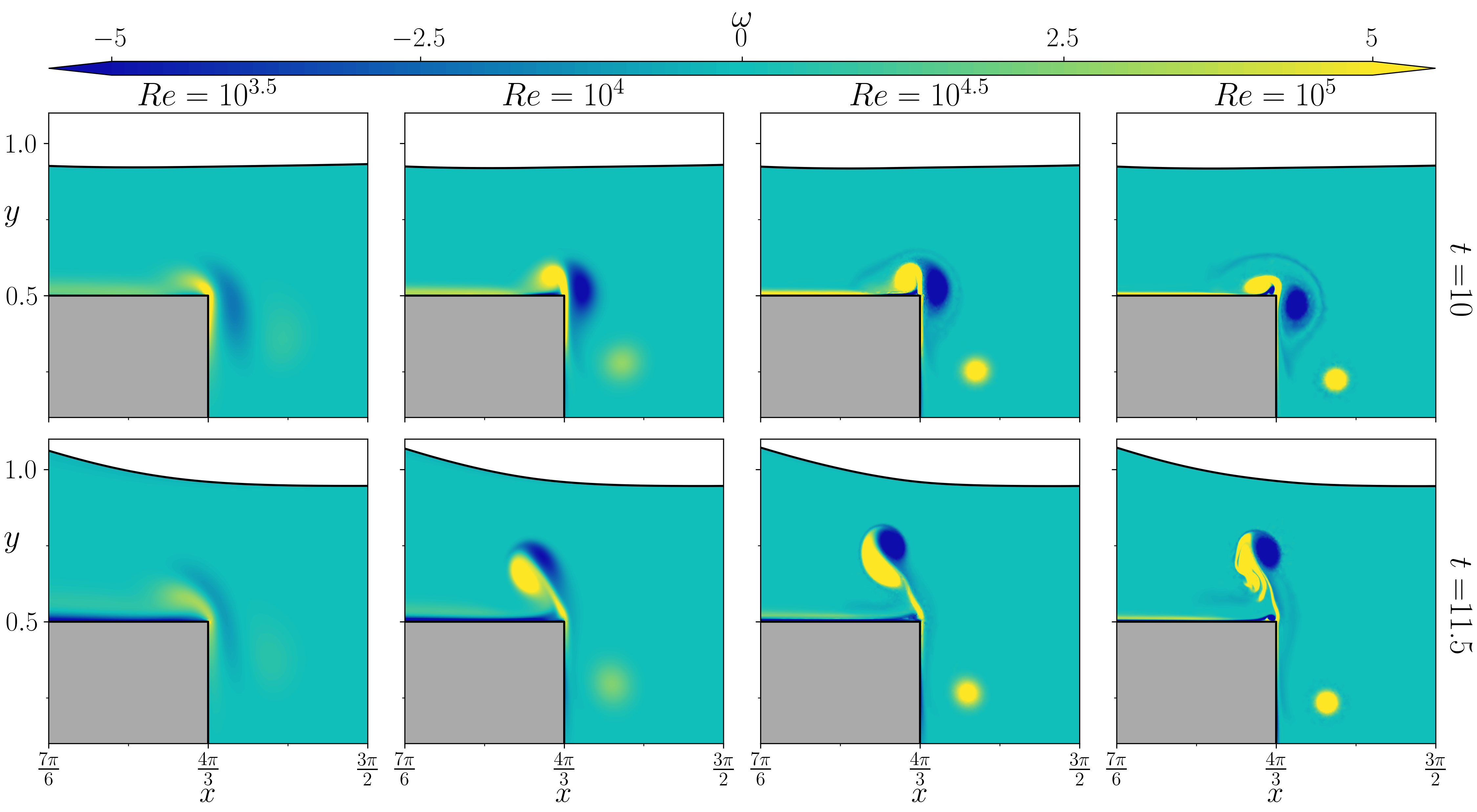
Figures (from R. & Dormy (2025, in press)) - The vorticity at fixed times \(t = 10\) and \(t = 11.5\) for \(\mathrm{Re} = 10^{3.5}\), \(10^4\), \(10^{4.5}\) and \(10^5\).

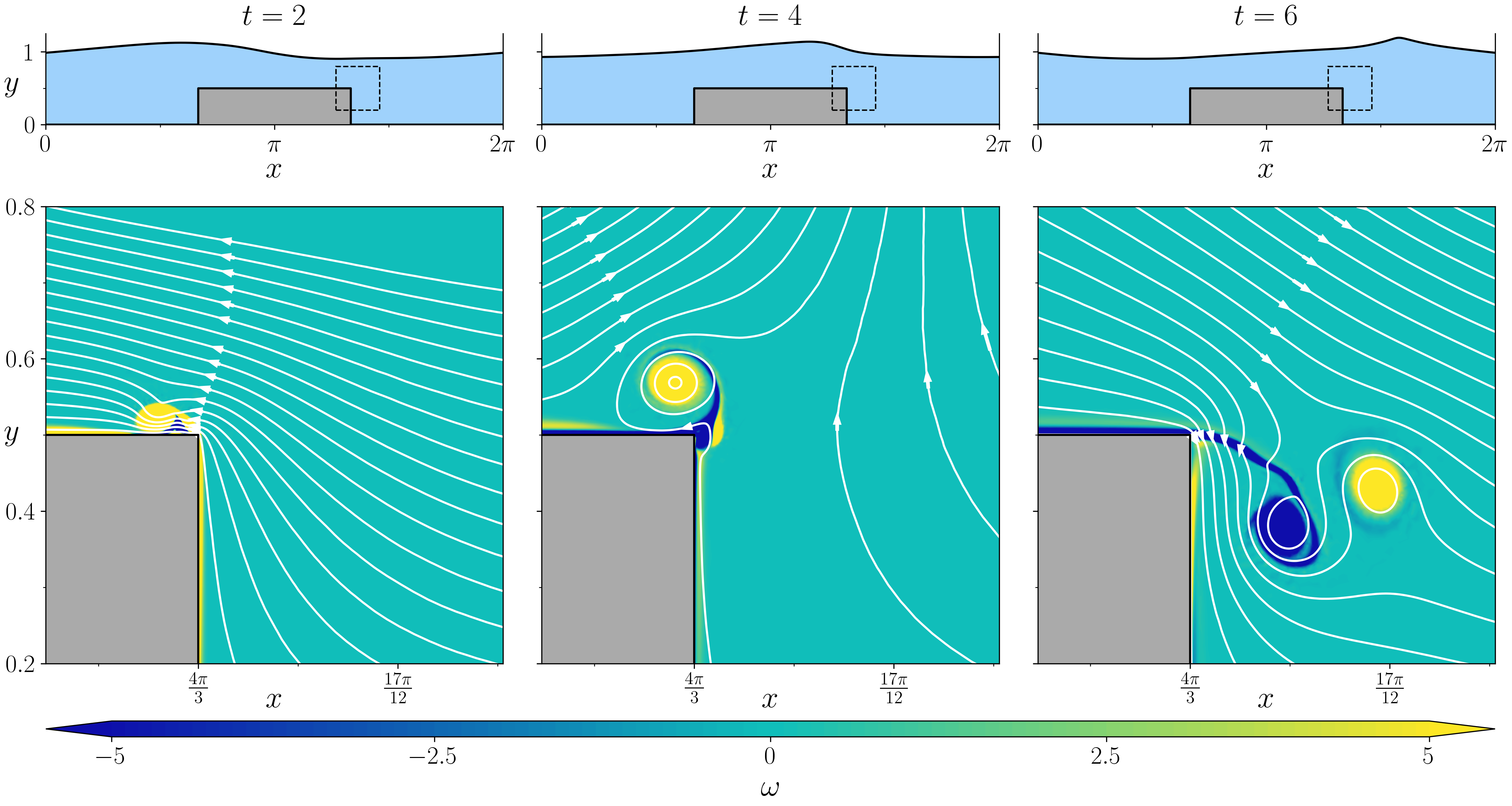
Figure (from R. & Dormy (2025, in press)) - Streamlines at \(\mathrm{Re} = 10^5\).

Animated Figure (from R. & Dormy (2025, in press)) - Vorticity evolution at \(\mathrm{Re} = 10^5\).

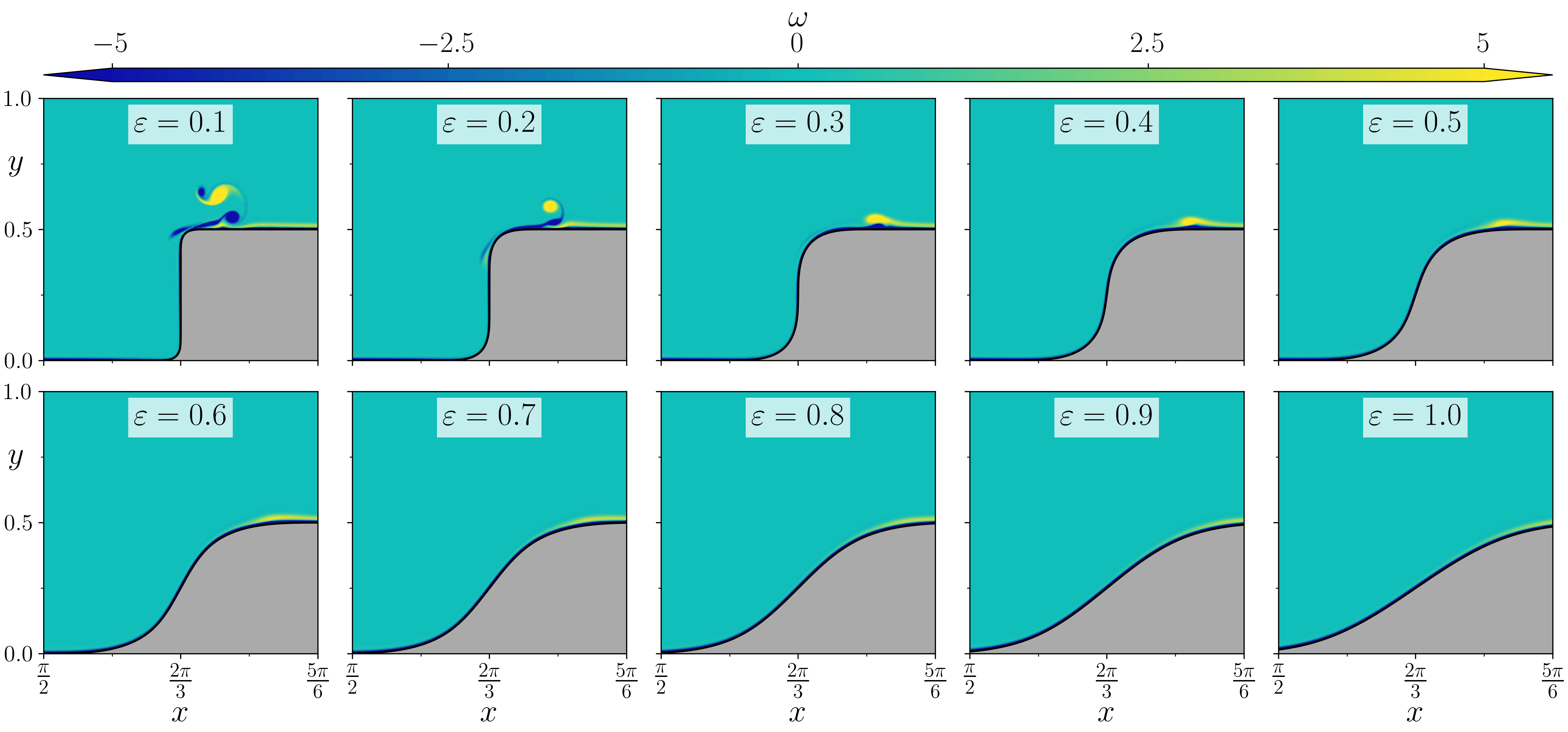
Figure (from R. & Dormy (2025, in press)) - Vorticity at fixed time \(t = 10\) with different curvature radii \(\varepsilon\).

Thank you!

Slides created using reveal.js

Drawings & animations created using Manim Community